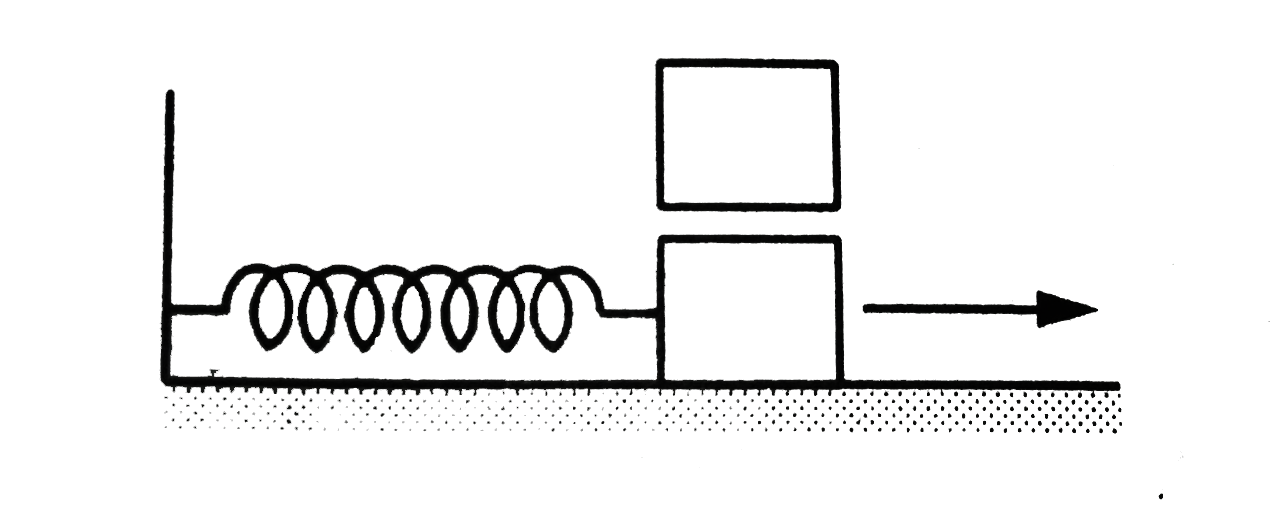
A 1kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring constant 100Nm−1. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency.
 Solution in Tamil
Solution in Tamil
The correct Answer is:B, C
Amplitude =0.1m
total mass =3+21=4kg ltbrrgt (when both the blocks are moving together)
K=100NM
∴T=2πmk
=2π√4100=2π5sec
∴Frequencey=52πHz
Again at the mean position let 1 kg block has velocity v
KE=12mv2=12kx2
Where xrarr Amplitude =0.1m
∴(12)×(1×v2)=(1×2)×100(0.1)2
Kv=1msec−1..........i
After the 3 kg block is gently place on teh 1 kg, then let 1kg+3kg-4kg block and the spring the be one system. For this mass spring system there is no extgernla force. (when oscillation takes place). The momentum should be conserved. Let 4 kg block has velocity v.
∴Intialmomentum=FiNAlmomentum<br>1xxv=4xxv^1<br>rarr v^1=1/4m/s<br>[as v=1 msec^-1
at its mean position
KEmean=12mv2
=(12)×4×(14)2=12×14
KEmean=(1/2)m^1v^2(1/2)4x(1/4)^2<br>=1/2xx1/4<br>whentheblocksarego∈g→theextremeposition,therewillbeonlypotentiale≠rgy.<br>:. PE=1/2kdelta^2=1/2xx1/4<br>whered→Newamplitude<br>:. 1/4=100delta^2<br>=d=sqrt((1/400))<br>=0.05m=5m<br>So, amplitude =5cm
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
16 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Select the correct statements
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View SolutionA block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Fnd the maximum force exerted by the spring on the block.
View SolutionA 1kg block is eecuting simpe hrmonic motion of ampliltude 0.1 m m on a smooth horizontal surface under the restoring force of a spring of sprign constant 100Nm^-1 . A block of mass 3 kg is gently placed on it at the instant it pases through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.
View SolutionA 1kg block is executing simple harmonic motion of amplitude 0.1m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N//m . A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together. Find the frequency and the amplitude of the motion.
View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks. .
View SolutionA block of mass 2kg executes simple harmonic motion under the reading from at a spring .The angular and the time period of motion are 0.2cm and 2πsec respectively Find the maximum force execute by the spring in the block.
View SolutionA horizontal spring block system of mass M executes simple haormonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
View SolutionA block of mass 4kg attached with spring of spring constant 100N/m is executing SHM of amplitude 0.1m on smooth horizontal surface as shown in figure. If another block of mass 5kg is gently placed on it, at the instant it passes through the mean position and new amplitude of motion is n−1 meter then find n. Assuming that two blocks always mvoe together .
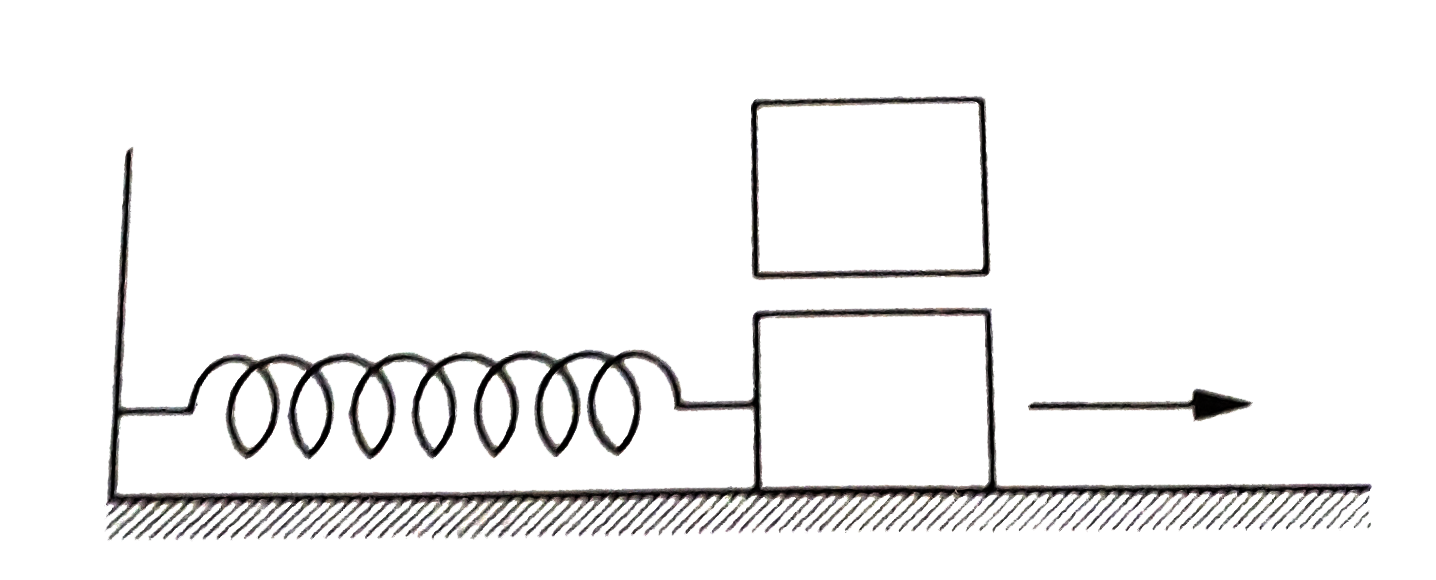
View Solutionएक चिकनी क्षैतिज सतह पर, एक किनारे पर बधे 100 N/m स्प्रिंग नियतांक वाले एक स्प्रिंग के बल के अधीन, 1 kg द्रव्यमान का एक ब्लॉक सरल आवर्त गति कर रहा है ब्लॉक की गति का आयाम 0.1 m है। जब यह ब्लॉक अपनी मध्य स्थिति से गुजर रहा होता है, 3kg का दूसरा ब्लॉक धीरे से इस पर रख दिया जाता है (चित्र 21.E12)। यह मानते हुए कि दोना साथ-साथ गति करते हैं, इस नई गति की आवृति तथा इसका आयाम निकाले
View SolutionA block of mass 2 kg executes SHM on a smooth horizontal plane under the action of restoring force of a spring. If the amplitude and time period of oscillation are 0.05 m and pi//5 second, the maximum force exerted by the spring on the block is
View SolutionA horizontal spring-block system of mass 1kg executes SHM of amplitude 10 cm. When the block is passing through its equilibrium position another mass of 1kg is put on it and the two move together.
View SolutionA block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
View SolutionA horizontal spring block system of mass 'm' executes SHM of amplitude 'A' and frequency 'n'. When the block passing through its equilibrium position, an object of mass 'm' is put on it and the two move together. Find the new amplitude
View SolutionA horizontal spring block system ( mass m_2 spring constant k) is oscillating on a smooth surface with amplitude A. If at the mean position an identical block is kept on it so that they move together after what is the new amplitude?
View Solution
