A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle $θ$ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is $μ$ . Find the range of the angular speed for which the block will not slip.Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

If et bowl rotates at maximum angular speed, the block tends to slip upwards.
So the frictioN/Al force acts downward.
Here, $r = R sin θ$
From the free body diagram 1
$R_{1} - m g cos θ - m ω^{2}_1 (R sin θ) sin θ$
$= 0 \dots \dots \dots . i$
[because $r = R sin θ]$ and
$μ R_{1} + m g sin θ - m ω^{2}_1 (R sin θ) cos θ$
=0 ii.

Substituting the value of $R_{1}$ from equation i. inequation ii it can be found out that
$ω_{1} = \frac{(g (sin θ) + μ cos θ)}{R sin θ (cos θ - μ sin θ)}]^{\frac{1}{2}}$
again, for minimum speed, the frictioN/Asl force $μ R_{2}$ acrts upwasrd,. From free body diagram -2, it can be prove that

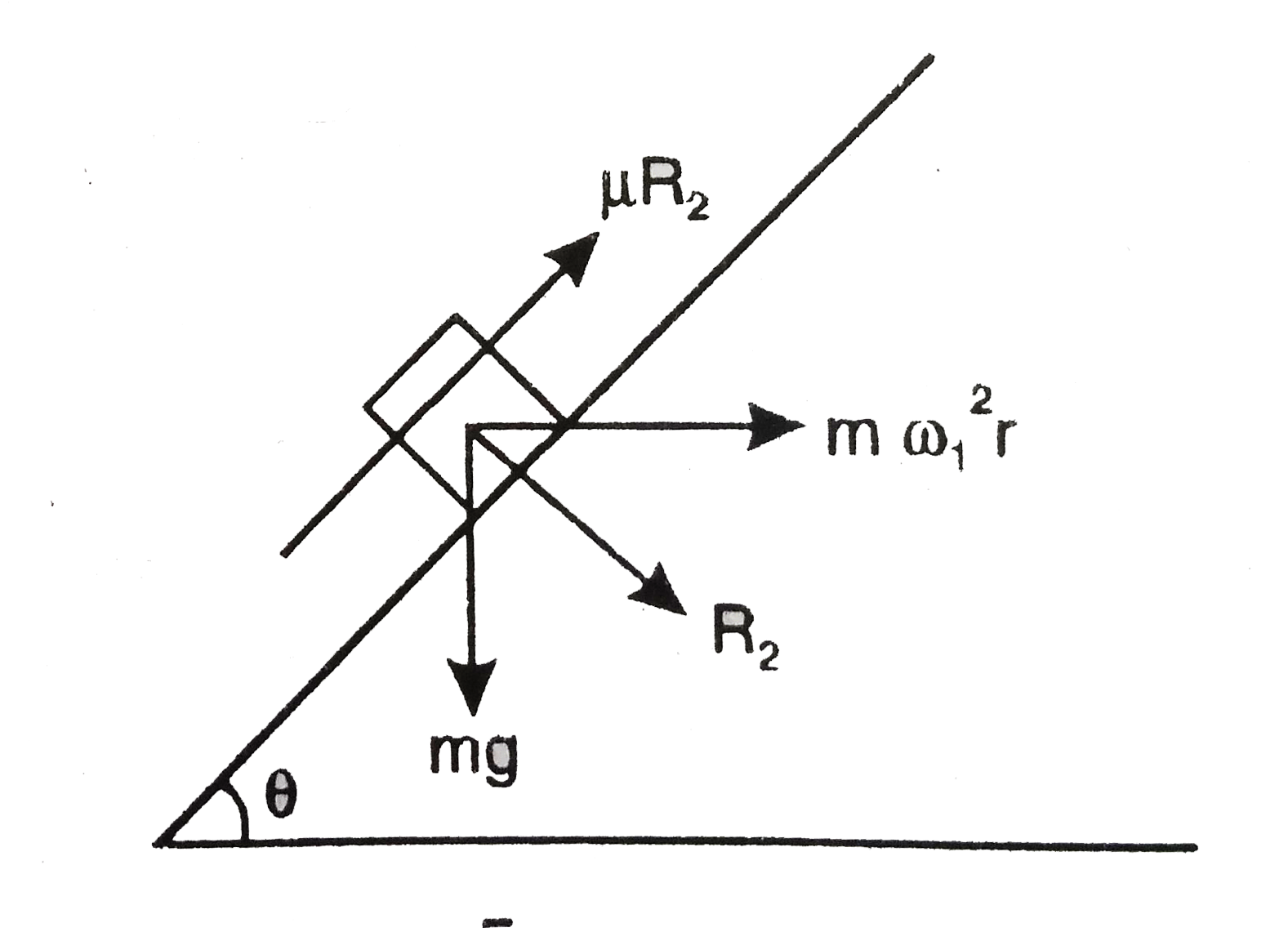
$ω_{2} = {[\frac{g (sin θ + μ cos θ)}{R sin θ (cos t h e t - μ sin θ)}]}^{\frac{1}{2}}$
$∴$ the range of speed is betwen $ω_{2} and ω_{1}$

Updated on:21/07/2023

|

Class 11 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

HC VERMA-CIRCULAR MOTION-Exercises

Home
Ask Doubt
Profile