AB and AC are the two tangents to a circle whose radius is 6 cm. If ∠BAC=60∘ , then what is the value (in cm) of √(AB2+AC2)?
6√6
4√6
9√3
8√3
The correct Answer is:A
Step by step video, text & image solution for AB and AC are the two tangents to a circle whose radius is 6 cm. If /_ BAC = 60^@ , then what is the value (in cm) of sqrt((AB^2 + AC^2 ))? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
AB and AC are the two tangets to a circle whose radius is 6cm. If ∠BAC=60∘, then what is the value (in cm) of √(AB2+AC2)?
View SolutionIn the given figure, AC and DE are perpendicular to tangent CB.AB passess through centre O of the circle whose radius is 20 cm. If AC=36 cm, what is the length (in cm) of DE?
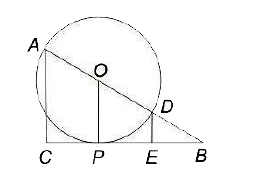
View Solution
Knowledge Check
In the given figure ,PR and ST are perpendiculars to tan- gent QR, PQ passes through centre O of the circle whose diameter is 10 cm . If PR = 9 cm what is the length (in cm.) of ST ?
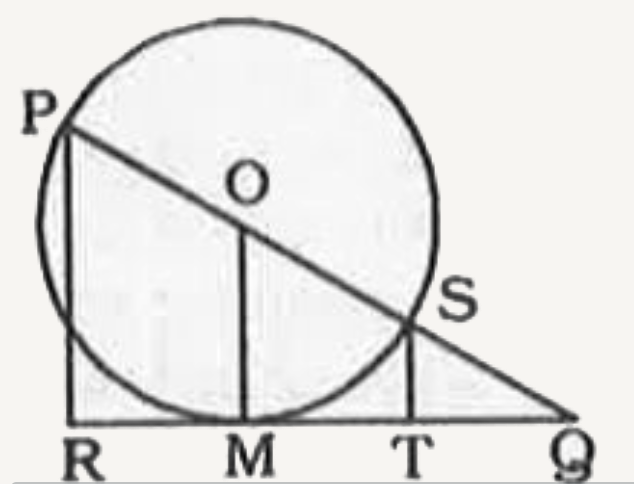 A4B6C2D8
A4B6C2D8In the given figure ,PR and ST are perpendiculars to tan- gent QR, PQ passes through centre O of the circle whose diameter is 10 cm . If PR = 9 cm what is the length (in cm.) of ST ?
 A4B6C2D8
A4B6C2D8AB is a tangent to a circle with centre O. If the radius at the circle is 7 cm and the length of AB is 24 cm, then what is the length (in cm) of OA?
A25B26C28D31
In Figure 2, AB and AC are tangents to the circle with centre O such that angle BAC = 40°. Then angle BOC is equal to
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionA, B and C are three points on the circle. If AB = AC= 7√2 cm and ∠BAC=90∘, then the radius is equal to:
वृत्त पर A, B और C तीन बिंदु हैं। यदि AB = AC = 72cm और ∠BAC=90∘ है, तो त्रिज्या है
View SolutionAB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionTwo tangents PA and PB are drawn from a point P to the circle. If the radius of the circle is 5 cm and AB = 6 cm and O is the centre of the circle. OP cuts AB at C and OC = 4 cm, then OP :-
View Solution
