5 सेमी. त्रिज्या वाले एक वृत्त कि दो जिवाएँ AB तथा AC इस प्रकार हैं कि AB=AC=6 सेमी. जीवा BC की लम्बाई ज्ञात करो।
हम जानते हैं कि यदि AB तथा AC किसी वृत्त कि दो समान लम्बाई की जिवाएँ हो, तो वृत्त का केन्द्र ∠BAC के अर्ध्दक पर स्थित होगा ।
यहाँ हमे दिया गया है कि AB = AC = 6 सेमी. है, तो ∠BAC का अर्ध्दक वृत्त के केन्द्र O से गुजरेगा अर्थात OA, ∠BAC का अर्ध्दक होगा । चूँकि समद्विबाहु त्रिभुज में शीर्ष कोण का अर्ध्दक सम्मुख भुजा पर लम्ब होता है तथा इसे समद्विभाजित करता है ।
∴ AM⊥BC तथा BM = BC

समकोण त्रिभुज AMB में
AB2=AM2+BM2
⇒ 36=AM2+BM2 [∵AB=6 सेमी.]
⇒ BM2=36−AM2 ...(i)
समकोण त्रिभुज OMB में
∴ OB2=OM2+BM2
⇒ 25=(OA−AM)2+BM2 [∵OB= त्रिज्या = 5 सेमी., OA = त्रिज्या = 5 सेमी. तथा OM + AM = OA = 5 सेमी.]
⇒ 25=(5−AM)2+BM2
⇒ BM2=25−(5−AM)2 ...(ii)
(i) तथा (ii) से
36−AM2=25−(5−AM)2
⇒ 36−AM2=25−(25−10AM+AM2)
⇒ 36−AM2=25−25+10AM−AM2
⇒ 10AM=36⇒AM=3.6 सेमी.
AM का मान (i) में रखने पर,
BM2=36−(3.6)2=36−12.96=23.04
⇒ BM=√23.04=4.8 सेमी.
⇒ BC=2BM=2×4.8=9.6 सेमी.
अत: जीवा BC की लम्बाई 9.6 सेमी. है ।
Related Playlists
- BOOK - RD SHARMACHAPTER - वृत्तEXERCISE - प्रश्नावली 16.116videos
वृत्त
- BOOK - RD SHARMACHAPTER - वृत्तEXERCISE - प्रश्नावली 16.215videos
वृत्त
- BOOK - RD SHARMACHAPTER - वास्तविक संख्याओं के घातांकEXERCISE - बहु विकल्पीय प्रश्न40videos
वास्तविक संख्याओं के घातांक
- BOOK - RD SHARMACHAPTER - संख्या पद्धति EXERCISE - बहु विकल्पीय प्रश्न21videos
संख्या पद्धति
Similar Questions
वे सभी बिन्दु जो एक वृत्त के अंदर/बाहर स्थित होते हैं, उन्हें …….. बिन्दु कहते हैं ।
01:56View Solutionएक वृत्त की त्रिज्या 8 सेमी. है । यदि इसकी एक जीवा की लम्बाई 12 सेमी. हो, तो इस जीवा की वृत्त के केंद्र से दूरी ज्ञात करो ।
03:18View Solution{2−3(2−3)3}3 का मान होगा:
02:53View Solutionनिम्न में से कौन सा कथन सत्य है?
05:53View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।
 07:04View Solution
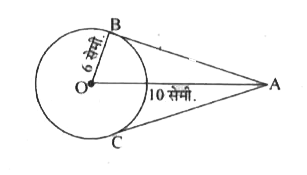
07:04View Solutionदिये गये चित्र में O वृत्त का केंद्र है। AB व AC वृत्त कि स्पर्श रेखाएं है। यदि OA=10 सेमी तथा OB=6 सेमी है तो AC कि लम्बाई लिखिए।
 06:39View Solution
06:39View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
02:52View Solutionएक 4 सेमी त्रिज्या का वृत्त खींचिए। उस पर दो स्पर्श रेखाएं इस प्रकार खींचिए कि वे परस्पर 70∘ का कोण बनती हो।
02:05View Solution2.5 सेमी का एक वृत्त खींचिए। वृत्त के केंद्र से 6.5 सेमी कि दूरी पर स्थित किसी बिंदु से वृत्त कि स्पर्श रेखाएं खींचिए। स्पर्श रेखाओ कि लम्बाई नापकर तथा गणना द्वारा ज्ञात कीजिए।
05:20View SolutionPQ रेखा 6 सेमी कि खींचिए। Q बिंदु से3.5 सेमी त्रिज्य का एक वृत्त खींचिए। बिंदु से इस वृत्त पर स्पर्श रेखाएं खींचिए। स्पर्श रेखाओ कि लम्बाई नापकर तहा गणना करके ज्ञात कीजिए।
03:09View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
01:48View SolutionIn a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is : O केंद्र वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:
02:48View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is : AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
02:04View SolutionIn triangle ABC , angle A is a right angle. The lengths of AC and BC 6 cm and 10 cm respectively. Point D is on AB such that BD = 4 cm. What is the length of CD? त्रिभुज ABC में, कोण A समकोण है | AC और BC की लंबाई क्रमशः 6 सेमी और 10 सेमी है | बिंदु D, AB पर इस प्रकार स्थित है कि BD = 4 सेमी है | CD की लंबाई ज्ञात करें |
03:42View SolutionIn a circle of radius 13 cm , a chord is at a distance of 12 cm from the centre of the circle. What is the length of the chord?
13 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 12 सेमी की दूरी पर एक जीवा है | जीवा की लंबाई ज्ञात करें |06:52View SolutionIn a circle of radius 17 cm, a chord is at a distance of 15 cm from the centre of the circle. What is the length of the chord?
17 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 15 सेमी की टूरी पर एक जीवा है| जीवा की लंबाई ज्ञात करें |02:01View Solution


