In PS is the bisector of and . If and then the measure of is
The correct Answer is:C
To solve the problem step by step, we will analyze the given triangle ΔPQR and apply the properties of angles and triangles.
Step 1: Write down the given information
- ∠SPT=28∘
- ∠R=23∘
- PS is the bisector of ∠P
- PT⊥PQ (meaning PT is perpendicular to PQ)
- ∠Q>∠R
Step 2: Understand the implications of the angle bisector
Since PS bisects ∠P, we can denote:
- ∠QPS=∠SPR=x
Thus, we have:
∠P=2x
Step 3: Analyze triangle PTS
In triangle PTS, we know:
- ∠SPT=28∘
- PT⊥PQ implies ∠PTS=90∘
Using the triangle angle sum property:
∠PTS+∠SPT+∠TSP=180∘
Substituting the known values:
90∘+28∘+∠TSP=180∘
This simplifies to:
∠TSP=180∘−118∘=62∘
Step 4: Find ∠PSR
Since PS bisects ∠P, we have:
∠PSR=180∘−∠TSP=180∘−62∘=118∘
Step 5: Analyze triangle PSR
In triangle PSR:
∠SPR+∠PSR+∠R=180∘
Substituting the known values:
∠SPR+118∘+23∘=180∘
This simplifies to:
∠SPR+141∘=180∘
Thus:
∠SPR=180∘−141∘=39∘
Step 6: Relate ∠Q to the angles found
Since PS bisects ∠P:
∠QPS=∠SPR=39∘
Now, we can find ∠Q:
∠Q=180∘−∠QPS−∠PSR
Substituting the known values:
∠Q=180∘−39∘−62∘
This simplifies to:
∠Q=180∘−101∘=79∘
Final Answer
Thus, the measure of ∠Q is 79∘.
---
- ∠SPT=28∘
- ∠R=23∘
- PS is the bisector of ∠P
- PT⊥PQ (meaning PT is perpendicular to PQ)
- ∠Q>∠R
Since PS bisects ∠P, we can denote:
- ∠QPS=∠SPR=x
∠P=2x
In triangle PTS, we know:
- ∠SPT=28∘
- PT⊥PQ implies ∠PTS=90∘
∠PTS+∠SPT+∠TSP=180∘
Substituting the known values:
90∘+28∘+∠TSP=180∘
This simplifies to:
∠TSP=180∘−118∘=62∘
Since PS bisects ∠P, we have:
∠PSR=180∘−∠TSP=180∘−62∘=118∘
In triangle PSR:
∠SPR+∠PSR+∠R=180∘
Substituting the known values:
∠SPR+118∘+23∘=180∘
This simplifies to:
∠SPR+141∘=180∘
Thus:
∠SPR=180∘−141∘=39∘
Since PS bisects ∠P:
∠QPS=∠SPR=39∘
Now, we can find ∠Q:
∠Q=180∘−∠QPS−∠PSR
Substituting the known values:
∠Q=180∘−39∘−62∘
This simplifies to:
∠Q=180∘−101∘=79∘
Thus, the measure of ∠Q is 79∘.
Similar Questions
In △PQR,∠Q≻∠R, PS is the bisector of ∠P and PT⊥QR. If ∠SPT=28∘ and ∠R=23∘ , then the measure of ∠Q is:
त्रिभुज PQR में, ∠Q≻∠R, है तथा PS कोण P का समद्विभाजक है और PT⊥QR है । यदि ∠SPT=28∘ और ∠R=23∘ है, तो कोण Q का मान क्या है?
View SolutionIn the Figure ΔPQR PT ⊥ QR at T and T FS is the bisector of ∠QPR if ∠PQR=78∘, and ∠TPS=24∘ then the measure of ∠PRQ is.
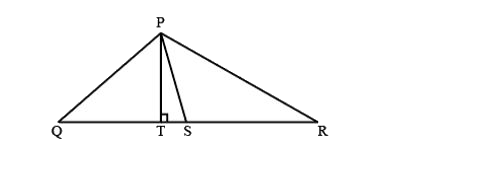
View Solution
Knowledge Check
In ΔPQR, Ps is the bisector of <P and PT⊥QR, then <TPS is equal to
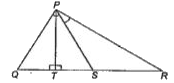 A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R)
A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R)In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
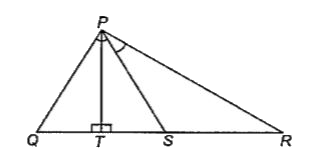 A10B30C60D15
A10B30C60D15In ΔPQT,PQ=PT. The points R and S are on QT such that PR = PS. If ∠PTS=62∘and∠RPS=34∘, then measure of ∠QPR is
A11∘B13∘C15∘D17∘
In the given figure, the bisectors of ∠P and ∠Q meet at a point A.If ∠R=110∘ and ∠S=50∘, find measure of ∠PAQ
View SolutionIn ΔPQR, ray PS is the bisector of ∠QPR.
Q−S−R. If QS=4.8cm,SR=3.6cm then find PQ:PR.
View SolutionIn ΔPQR, ray PS is the bisector of ∠QPR, Q−S−R. If Qs=4.8cm, SR=3.6cm, find PQ:PR.
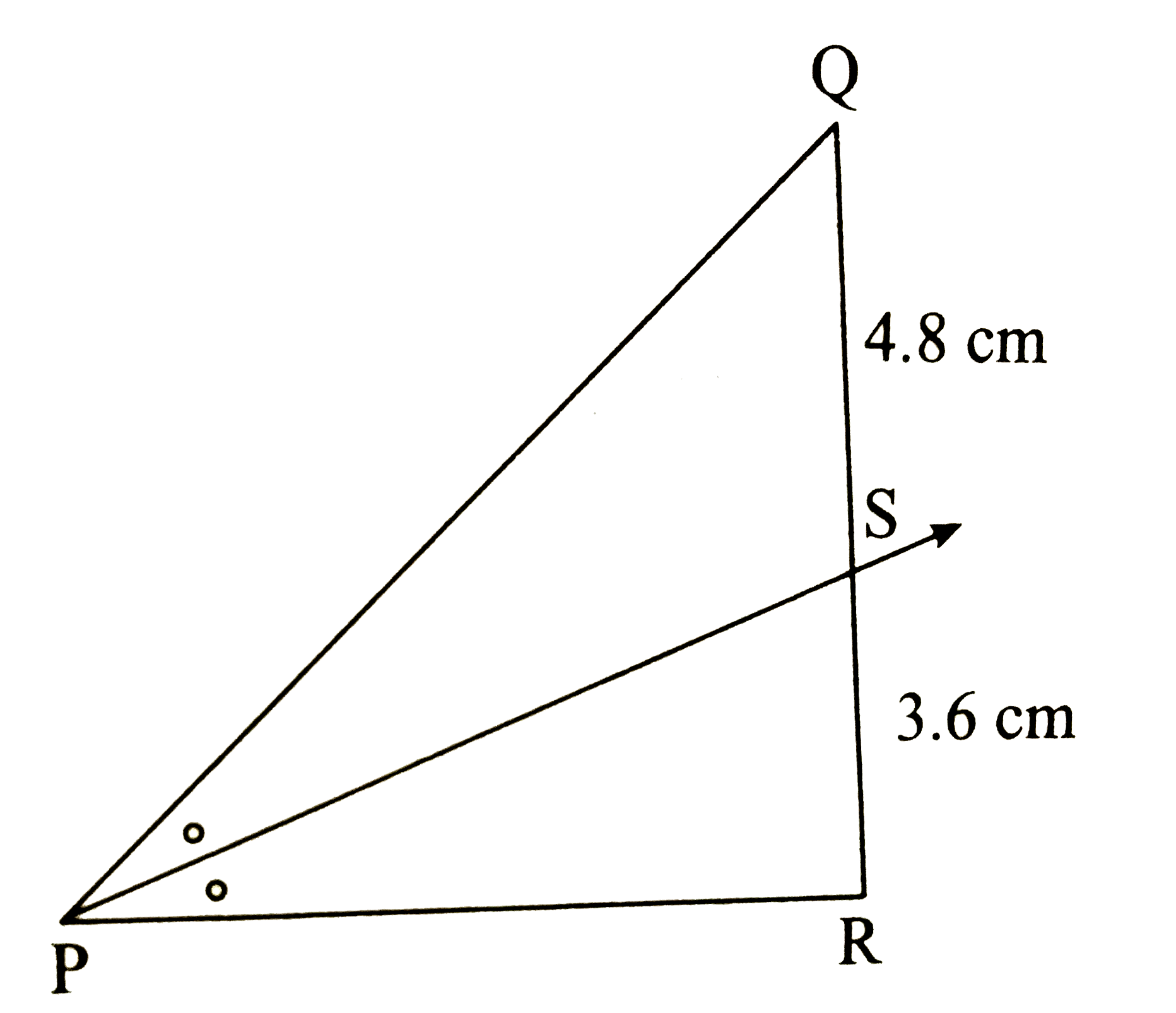
View SolutionIn Figure PS is the bisector of ∠QPR and PT⊥QR . Show that ∠TPS=12(∠Q−∠R).
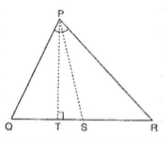
View SolutionIn Figure PS is the bisector of ∠QPR and PT ⊥QR . Show that ∠TPS=12(∠Q−∠R)
View Solution
