यदि px4+qx3+rx2+sx+f=
∣∣
∣
∣∣x2+3xx−1x+3x+12−xx−4x−3x+43x∣∣
∣
∣∣ तो
दर्शाइए कि f=18.
The correct Answer is:71
Step by step video, text & image solution for यदि px^(4)+qx^(3)+rx^(2)+sx+f= |(x^(2)+3x,x-1,x+3),(x+1,2-x,x-4),(x-3,x+4,3x)| तो दर्शाइए कि f=18. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
तीन अलग - अलग क्षणों पर सूर्य की किरणों द्वारा h ऊंचाई के एक ऊर्ध्वाधर खंभे की छाया की लंबाई b, 2h और 3h हैं। इन तीनों क्षणों पर किरणों के उन्नयन कोणों का योग बराबर है:
View Solutionसदिश 3→a−5→b और 2→a+→b परस्पर लंबवत हैं तथा सदिश →a+4→b और −→a+→b भी परस्पर लंबवत हैं। तब, सदिशों के →a और →b के बीच का कोण है
View SolutionIf f(x)=ax^(2)+bx+c and g(x)+px^(2)+qx with g(1)=f(1)g(2)-f(2)=1g(3)-f(3)=4 then g(4)-f(4) is
View SolutionFind the intervals in which the following function are increasing or decreasing. f(x)=10−6x−2x2 f(x)=x2+2x−5 f(x)=6−9x−x2 f(x)=2x3−12x2+18x+15 f(x)=5+36x+3x2−2x3 f(x)=8+36x+3x2−2x3 f(x)=5x3−15x2−120x+3 f(x)=x3−6x2−36x+2 f(x)=2x3−15x2+36x+1 f(x)=2x3+9x2+20 f(x)=2x3−9x2+12x−5 f(x)=6+12x+3x2−2x3 f(x)=2x3−24x+107 f(x)=−2x3−9x2−12x+1 f(x)=(x−1)(x−2)2 f(x)=x3−12x2+36x+17 f(x)=2x3−24+7 f(x)=310x4−45x3−3x2+365x+11 f(x)=x4−4x f(x)=x44+23x3−52x2−6x+7 f(x)=x4−4x3+4x2+15 f(x)=5x32−3x52,x>0 f(x)==x8+6x2 f(x)==x3−6x2+9x+15 f(x)={x(x−2)}2 f(x)=3x4−4x3−12x2+5 f(x)=32x4−4x3−45x2+51 f(x)=log(2+x)−2x2+x,xR
View SolutionIf px^4+qx^3+rx^2+sx+t=|(x^2+3x,x-1,x+3),(x+1,2-x,x-3),(x-3,x+4,3x)| then t is equal to
View SolutionThe function f(x)=[|x-3,x<=1 and ((x^(2))/(4))-((3x)/(2))+((13)/(4)),x<1 is
View Solution|[x^2+3,x-1,x+3],[x+1,-2x,x-4],[x-3,x+4,3x]|=px^4+Qx^3+rx^2+sx+t
View SolutionSTATEMENT-1 : If f(3x−43x+4)=x+2, then ∫f(x)dx is equal to 23x−83log|x−1|+c.
and
STATEMENT-2 : If f(3x−43x+4)=x+2, then f(x)=23−83(x−1).
View Solutionयदि px4+qx3+rx2+sx+f=
∣∣ ∣ ∣∣x2+3xx−1x+3x+12−xx−4x−3x+43x∣∣ ∣ ∣∣ तो
दर्शाइए कि f=18.
View SolutionLet px4+qx3+rx2+sx+t=∣∣ ∣ ∣∣x2+3xx−1x+3x+1−2x−4x−3x+43x∣∣ ∣ ∣∣ be an identity where p,q,r,s and t are constants, then the value of s is equal to
View SolutionIf px^(4)+qx^(3)+rx^(2)+sx+t=|{:(x^(2)+3x,x-1,x+3),(x^(2)+1,2-x,x-3),(x^(2)-3,x+4,3x):}| then t is equal to
View Solutionफलन f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x2यदिx<1xयदि1≤x<2x34यदिx≥2,तब x=2 पर ,f(x) के सांतत्य का परीक्षण कीजिए।
View Solutionयदि f(x)=x3−x2+3x+4 तो मान निकालें f(2) और f(−13) का मान निकालें।
View SolutionIf f(x) = ∫3x+2x4−x3+x2−1dx then f(x) has
View Solutionयदि ∣∣ ∣ ∣∣1+xxx2x1+xx2x2x1+x∣∣ ∣ ∣∣=px5+qx4+rx3+sx2+tx+w, तब
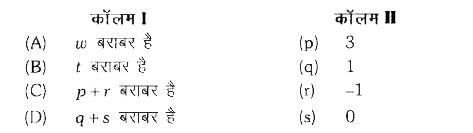
View Solutionयदि ∣∣ ∣ ∣∣x2+3xx−1x+3x+1−2xx−4x−3x+43x∣∣ ∣ ∣∣=px4+qx3+rx2+sx+t जहाँ p,q,r,s व t अचर हैं, तो t का मान होगा
View Solution
