यदि ∣∣
∣
∣∣1+xxx2x1+xx2x2x1+x∣∣
∣
∣∣=px5+qx4+rx3+sx2+tx+w, तब
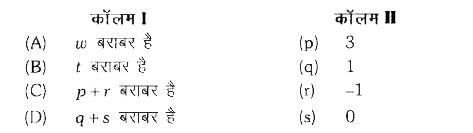
The correct Answer is:A, B, C, D
Step by step video, text & image solution for यदि |(1+x,x,x^(2)),(x,1+x,x^(2)),(x^(2),x,1+x)|=px^(5)+qx^(4)+rx^(3)+sx^(2)+tx+w, तब by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
माना A=[aij] एक n×n कोटि का आव्यूह है A का अभिलाक्षणिक आव्यूह A−λI है, जहाँ λ अदिश है तथा I एक तत्समक आव्यूह है λ के रूप में सारणिक |A−λI|,n घात का अशून्य बहुपद है जिसे A का अभिलाक्षणिक बुहपद कहा जाता है, |A−λI|=0 को आव्यूह A का अभिलाक्षणिक समीकरण कहते है। इसके मुलो को अभिलाक्षणिक मूल या गुप्त मूल या आइगन मान कहते है आव्यूह A को सभी आइगन मानों का समुच्चय A का स्पेक्ट्रम कहलाता है। आव्यूह A के आइगन मानों के गुणज सारणिक A के बराबर है।
आव्यूह A=⎡⎢⎣102012120⎤⎥⎦ के अभिलाक्षणिक मूल है01:37View Solution
04:39View SolutionIf px^4+qx^3+rx^2+sx+t=|(x^2+3x,x-1,x+3),(x+1,2-x,x-3),(x-3,x+4,3x)| then t is equal to
02:11View Solution|[x^2+3,x-1,x+3],[x+1,-2x,x-4],[x-3,x+4,3x]|=px^4+Qx^3+rx^2+sx+t
05:41View SolutionDetermine the point of symmetry of a regular hexagon.
02:10View SolutionMatch the following Column A to Column B
02:50View SolutionThe inequation represented by the graph given below is :
01:13View SolutionIn fig. O is the center of the circle. Find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_031_Q01.png" width="80%"gt01:50View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt01:10View SolutionAt x=0, value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_024_Q01.png" width="80%"gt
02:54View SolutionIf y-x=180^(@) then find the values of x and y. ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_034_Q01.png" width="80%"gt
10:03View Solutionयदि px4+qx3+rx2+sx+f=
∣∣ ∣ ∣∣x2+3xx−1x+3x+12−xx−4x−3x+43x∣∣ ∣ ∣∣ तो
दर्शाइए कि f=18.01:59View SolutionLet px4+qx3+rx2+sx+t=∣∣ ∣ ∣∣x2+3xx−1x+3x+1−2x−4x−3x+43x∣∣ ∣ ∣∣ be an identity where p,q,r,s and t are constants, then the value of s is equal to
04:46View SolutionIf px^(4)+qx^(3)+rx^(2)+sx+t=|{:(x^(2)+3x,x-1,x+3),(x^(2)+1,2-x,x-3),(x^(2)-3,x+4,3x):}| then t is equal to
02:52View SolutionSuppose ∣∣ ∣ ∣∣1+xxx2x1+xx2x2x1+x∣∣ ∣ ∣∣=Px5+Qx4+Rx3+Mx2+Nx+Z be an identify in x ∀,P,Q,R,M,N,Z independent of x, then
01:26View Solution