In ΔABC, XY is parallel to BC and it divides the triangle into two equal areas (X lies on AB and Y lies on AC) then BX:AB equals
√2:√2−1
1:1
2:1
√2−1:√2
The correct Answer is:D
To solve the problem, we need to find the ratio BX:AB in triangle ABC where line XY is parallel to BC and divides the triangle into two equal areas. Here’s a step-by-step solution:
Step 1: Understand the Geometry
In triangle ABC, line XY is drawn parallel to side BC, intersecting AB at point X and AC at point Y. Since XY is parallel to BC, triangles AXY and ABC are similar.
Hint: Remember that when two lines are parallel, corresponding angles are equal, which implies similarity of triangles.
Step 2: Set Up Area Relationships
Since XY divides triangle ABC into two equal areas, we can denote the area of triangle AXY as 1 unit and the area of triangle ABC as 2 units.
Hint: The total area of triangle ABC is the sum of the areas of triangles AXY and XYB.
Step 3: Use the Area Ratio to Find Side Ratios
The ratio of the areas of similar triangles is equal to the square of the ratio of their corresponding sides. Thus, we have:
Area(ABC)Area(AXY)=21=2
This implies:
(ABAX)2=2
Taking the square root gives:
ABAX=√2
Hint: When dealing with similar triangles, remember that the ratio of areas relates to the square of the ratio of their corresponding sides.
Step 4: Express BX in Terms of AB
Let BX=x and AX=AB−x. From the ratio we found:
ABAX=√2⟹AX=AB√2
Now substituting AX:
AB−x=AB√2
Rearranging gives:
x=AB−AB√2=AB(1−1√2)
Hint: Rearranging equations can help isolate the variable you need.
Step 5: Find the Ratio BX:AB
Now we can express the ratio BX:AB:
BX=AB(1−1√2)
Thus, the ratio BX:AB becomes:
BX:AB=(1−1√2):1
Hint: When finding ratios, ensure both parts of the ratio are in terms of the same variable.
Final Answer
The ratio BX:AB is:
BX:AB=(1−1√2):1
This can be simplified further, but the essential form is established.
In triangle ABC, line XY is drawn parallel to side BC, intersecting AB at point X and AC at point Y. Since XY is parallel to BC, triangles AXY and ABC are similar.
Since XY divides triangle ABC into two equal areas, we can denote the area of triangle AXY as 1 unit and the area of triangle ABC as 2 units.
The ratio of the areas of similar triangles is equal to the square of the ratio of their corresponding sides. Thus, we have:
Let BX=x and AX=AB−x. From the ratio we found:
Now we can express the ratio BX:AB:
The ratio BX:AB is:
Topper's Solved these Questions
- CONGRUENCE AND SIMILAR TRIANGLES Book:LUCENT PUBLICATIONChapter:CONGRUENCE AND SIMILAR TRIANGLES Exercise:EXERCISE-5B
Explore 8 Videos
- CONGRUENCE AND SIMILAR TRIANGLES Book:LUCENT PUBLICATIONChapter:CONGRUENCE AND SIMILAR TRIANGLES Exercise:EXERCISE-5B
Explore 8 Videos
- CIRCLE AND ITS TANGENT LINESBook:LUCENT PUBLICATIONChapter:CIRCLE AND ITS TANGENT LINESExercise:EXERCISE 8B
Explore 27 Videos
- ELEMENTARY TRIGONOMETRIC IDENTITIES Book:LUCENT PUBLICATIONChapter:ELEMENTARY TRIGONOMETRIC IDENTITIES Exercise:EXERCISE 11B
Explore 37 Videos
Similar Questions
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
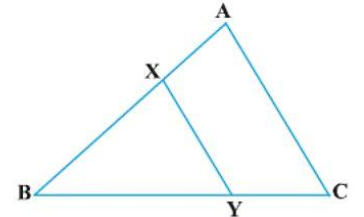
View SolutionIn the given figure, line the segment XY is parallel to side AC of ΔABC and it divides the triangles into two parts of equal area. Prove that AX:AB=(2−√2):2
View Solution
Knowledge Check
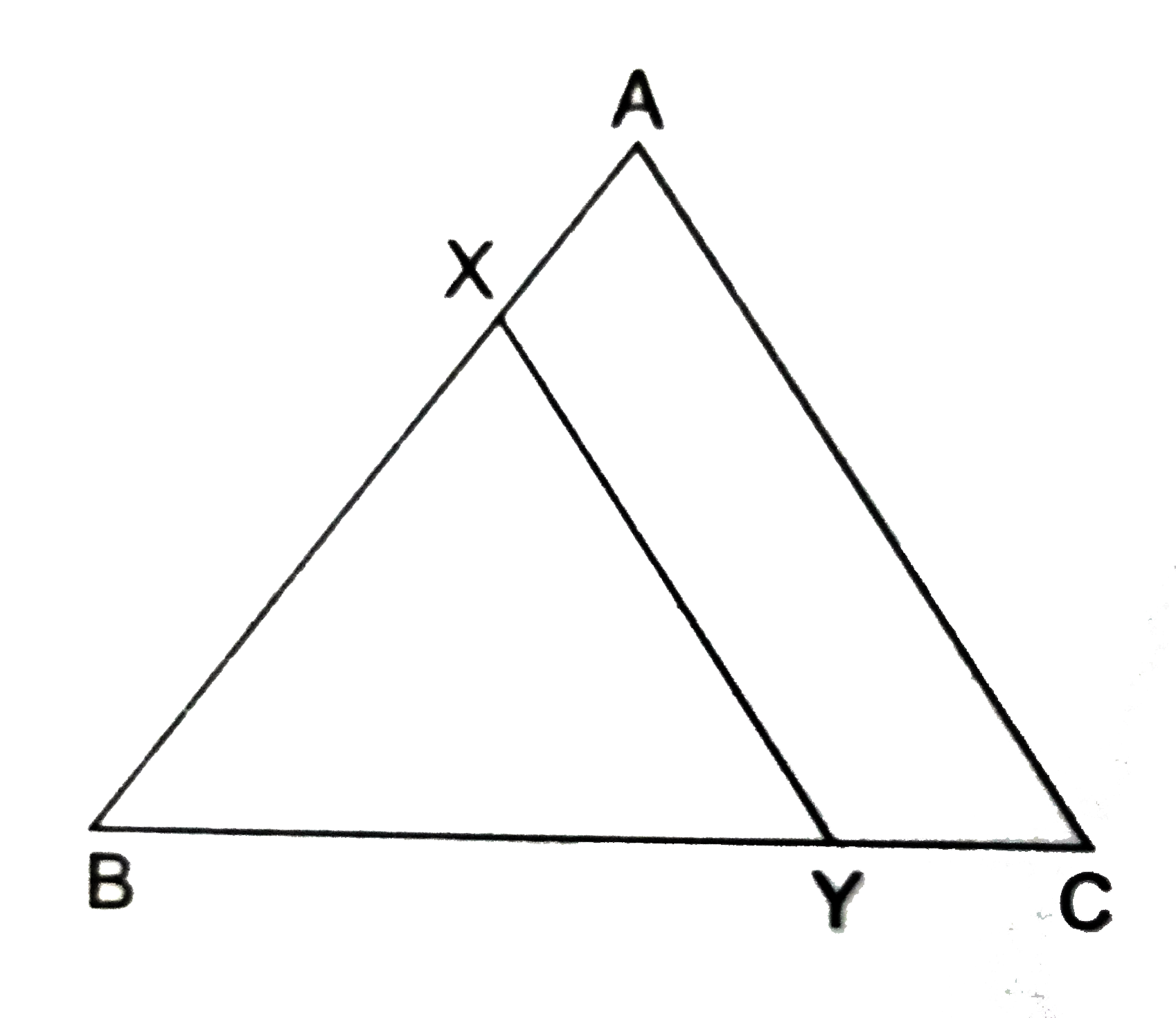
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
A√2+1+√2B2−√2:2C1:√2D1:1In the figure given below, XY parallel to AC. If XY divides the triangle into equal Parts, then value of AX/ AB is equal to
 A12B1√2C√2+1√2D√2−1√2
A12B1√2C√2+1√2D√2−1√2In △ABC, F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD⊥BC and AD intersect FE at G, then GD: AG = ?
△ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD⊥BC है और AD, FE को G पर काटती है, तो GD: AG = ?A√2:1B(√2−1):1C2√2:1D(√2+1):1
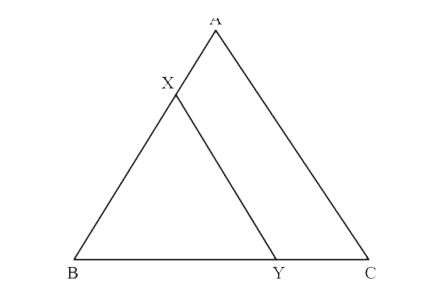
In the given figure, the line segment XY is Parallel to AC of ΔABC and it divides the triangle into two parts of equal areas. Prove that AXAB=√2−1√2
View SolutionIn triangle ABC, DE||BC where D is a point on AB and E is a point on AC. DE divides the area of △ABC into two equal parts.Then DB : AB is equal to
एक त्रिभुज ABC DE||BC है जिसमें D,AB पर एक बिंदू है और E, AC पर एक बिंदू है। DE, △ABC के क्षेत्रफल को दो समान भागों में विभाजित करता है, DB : AB किसके बराबर हे?
View SolutionIn ΔABC seg MN∣∣ side AC. Seg MN divides ΔABC into two parts equal in area. Determine MBAB.
View SolutionIn △ABC, F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD⊥BC and AD intersect FE at G, then GD: AG = ?
△ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD⊥BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View SolutionIn ΔABC, D and E are points on AB and AC respectively such that DE||BC and DE divides the ΔABC into two parts of equal areas. Then ratio of AD and BD is
View Solution