In the given figure, line the segment XY is parallel to side AC of ΔABC and it divides the triangles into two parts of equal area. Prove that AX:AB=(2−√2):2
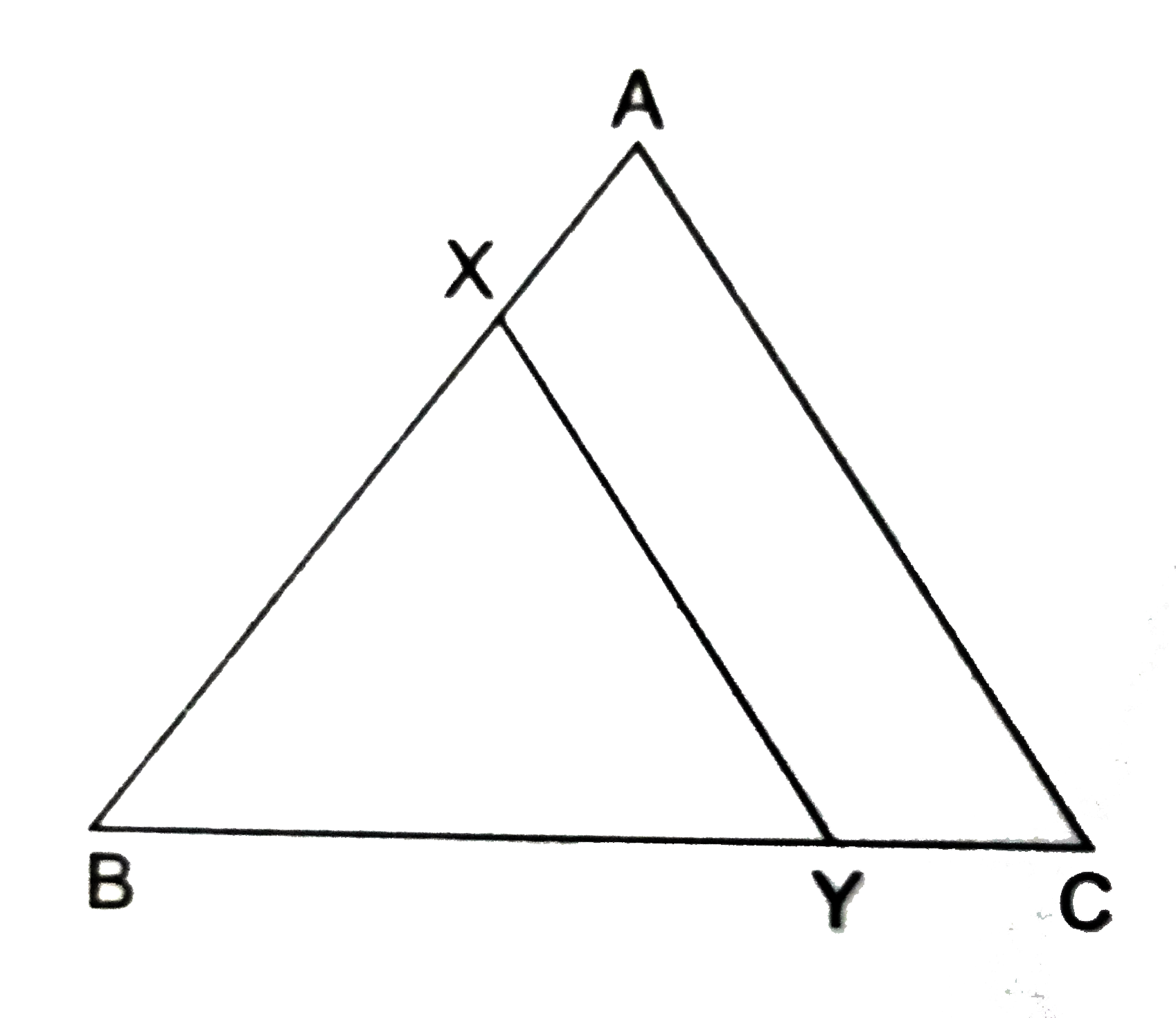
Since XY∣∣AC, we have,
∠A=∠BXYand∠C=∠BYX [ coress ∠]
∴ΔABC~ΔXBY
⇒ar(ΔABC)ar(ΔXBY)=AB2XB2....(i)
But, ar(ΔABC)~2×ar(ΔXBY) [ given]
⇒arΔABCar(ΔXYB)=2 ....(ii)
From (i) and (ii), we get
AB2XB2=2⇒(ABXB)2=2
⇒ABXB=√2AB=√2(XB)
⇒AB=√2(AB−AX)
⇒AXAB=√2(−1)√2×√2√2=(2−√2)2
Hence, AX:AB(2−√2):2
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
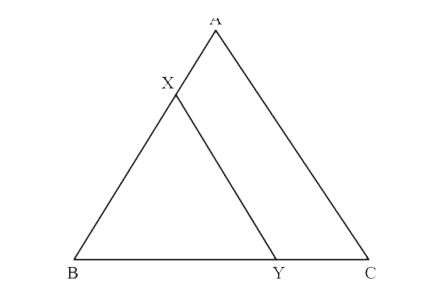
In the given figure, the line segment XY is Parallel to AC of ΔABC and it divides the triangle into two parts of equal areas. Prove that AXAB=√2−1√2
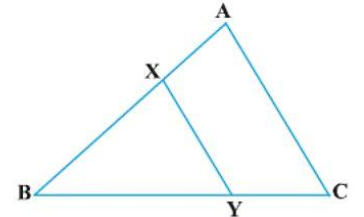
View SolutionIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
View Solution
Knowledge Check
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
A√2+1+√2B2−√2:2C1:√2D1:1In the figure given below, XY parallel to AC. If XY divides the triangle into equal Parts, then value of AX/ AB is equal to
 A12B1√2C√2+1√2D√2−1√2
A12B1√2C√2+1√2D√2−1√2In ΔABC, XY is parallel to BC and it divides the triangle into two equal areas (X lies on AB and Y lies on AC) then BX:AB equals
A√2:√2−1B1:1C2:1D√2−1:√2
In Fig. 4.176, XYAC and XY divides triangular region ABC into two parts equal in area. Determine AXAB.
View SolutionIn the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangle ABC and BQP are equal

View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
View SolutionX and Y are points on the sides AB and BC respectively of △ABC such that XY||AC and XY divides △ABC into two parts in area , find AXAB
View SolutionIn the given figure, XY∣∣ACandXY divides ΔABC into two regions, equal in area. Find the value of AXAB
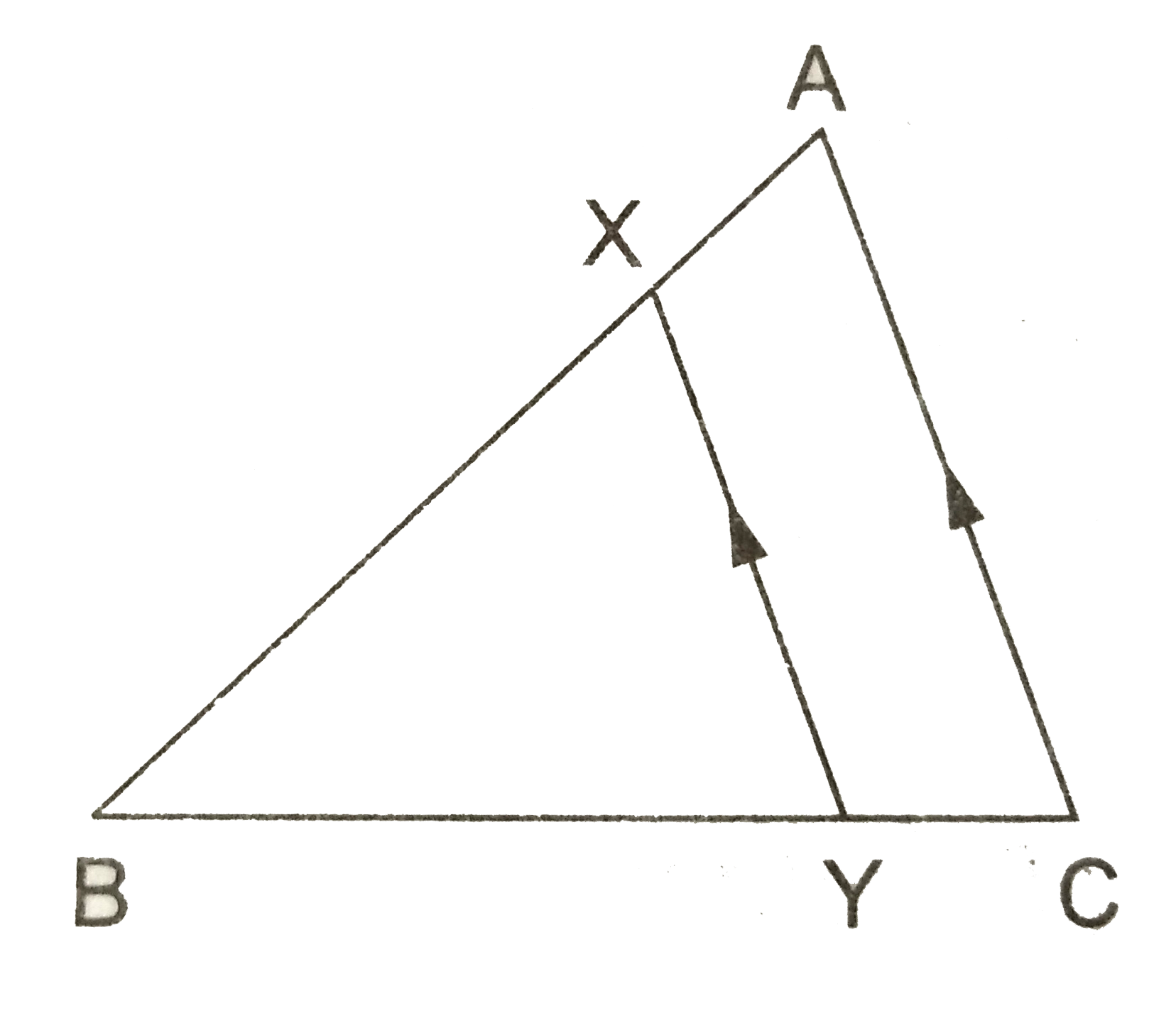
View Solution

