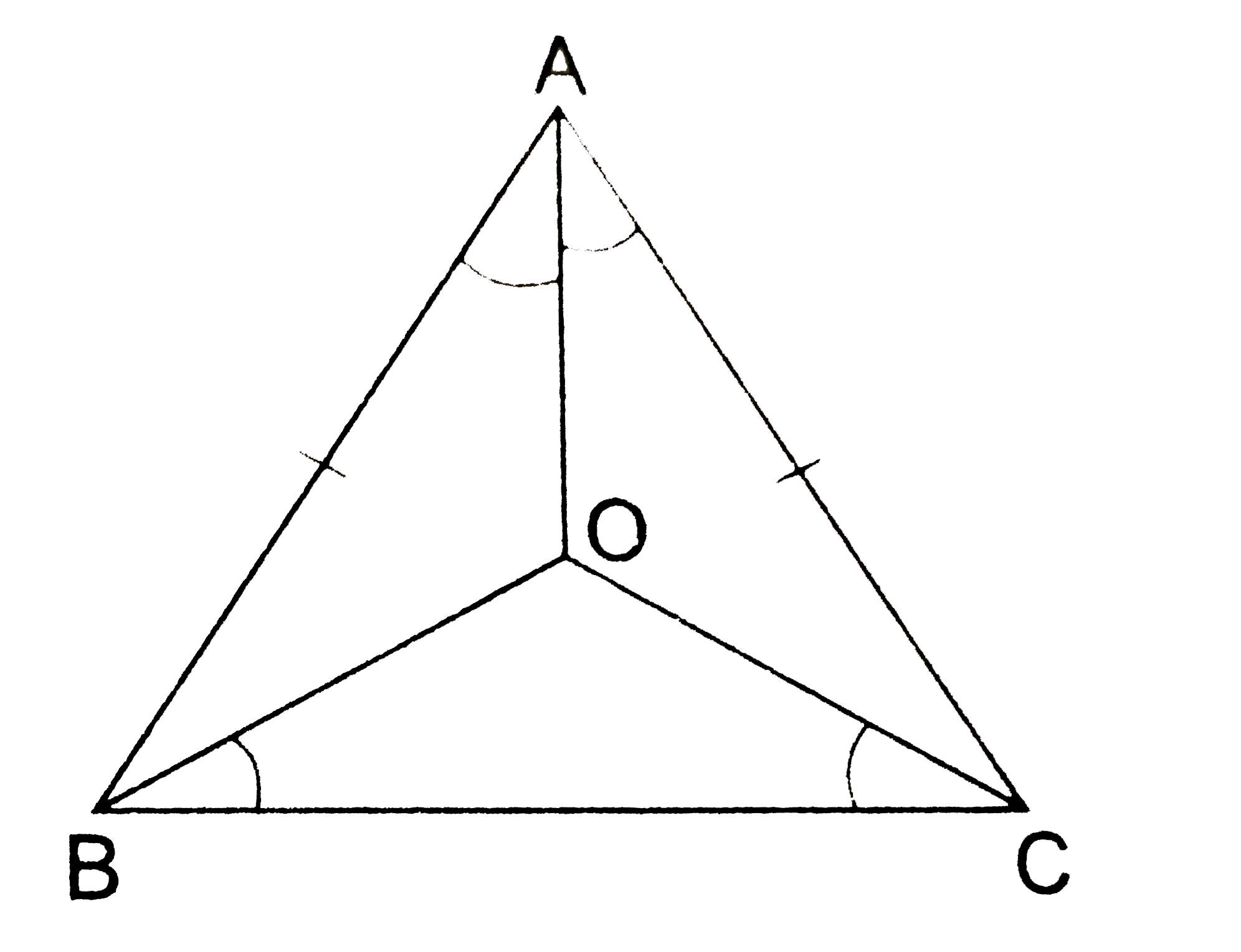
Triangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
AO is bisector of ∠A
The correct Answer is:BFFE=BEEC
Step by step video, text & image solution for Triangle ABC is an isosceles triangle with AB=AC. Bisectors of angleB and angleC intersect each other at O. join A-O and prove that AO is bisector of angleA by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5A47videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - ELEMENTARY TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE 11B37videos
ELEMENTARY TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
A36∘B32∘C28∘D40∘
In an isosceles triangle ABC, with AB=AC, the bisectors of B and C intersect each other at O. Join A to O. Show that :
(i) OB=OC
(ii) AO bisects AView SolutionABC is an isosceles triangle with AB = AC. Draw AP⊥BC to show that ∠B=∠C.
 View Solution
View SolutionIn ΔABC,AB=AC and the bisectors of ∠Band∠C meet at a point O. Prove that BO = CO and the ray AO is the bisector of ∠A.
 View Solution
View SolutionIn ABC, AB=AC, and the bisectors of angles B and C intersect at point O. Prove that BO=CO and the ray AO is the bisector of angle BAC
Since the angles opposite to equal sides are equal,
AB=AC
⇒∠C=∠B
⇒2∠B=2∠C
Since BO and CO are bisectors of ∠Band∠C, we also have
∠ABO=2∠B
∠ACO=2∠C
∠ABO=2∠B=2∠C=∠ACO.
Consider △BCO:∠OBC=∠OCB
BO=CO(Sides opposite to equal angles are equal)
Finally, consider triangles ABO and ACO.
BA=CA(given)
BO=CO(proved)
∠ABO=∠ACO (proved)
Hence, by S.A.S postulate△ABO≅△ACO
∠BAO=∠CAO
AObisects∠A.View SolutionIn ABC,AB=AC, and the bisectors of angles B and C intersect at point O . Prove that BO=CO and the ray AO is the bisector of angles BAC.
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View SolutionIn an isosceles ΔABC if ∠A=90∘ and AB=AC, find ∠B and ∠C.
View Solution
