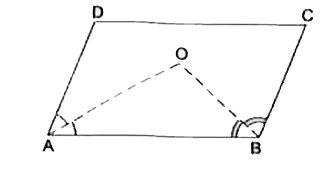
In a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
Video Solution
Text Solution
AP is the bisector of ∠A.
∴ ∠DAB=2∠PAB ...(1)
similarly, ∠CBA=2∠PBA ...(2)
We know that
∠CBA+∠CBA=180∘ (sum of co-interior angles of a parallelogram is180∘)
⇒ ∠PAB+∠PBA=90∘ [from(1)and(2)]
In∠APB, ...(3)
∠PAB+∠PBA+∠APB=180∘
⇒ 90∘+∠APB=180∘
⇒ ∠APB=180∘−90∘ (anglesumpoperty)
⇒ ∠APB=90∘ [from(3)]
|
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
Knowledge Check
In a ΔABC, the bisectors of ∠Band∠C intersect each other point O. Then∠BOC is ?
A∠BOC=180∘+12∠A.B∠BOC=90∘+12∠A.C∠BOC=180∘−12∠A.D∠BOC=90∘−12∠A.In parallelogram ABCD, bisectors of angles A and B intersect each other at "O" the value of angle AOB is.
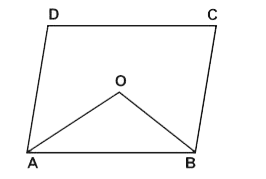 A90∘B30∘C60∘D120∘
A90∘B30∘C60∘D120∘In a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
A90∘B60∘C120∘Ddata insufficient
In a parallelogram ABCD, the bisector of ∠A bisects the line Bcat point X. Prove that AD = 2AB.
View SolutionIn the figure the bisectors of ∠P and ∠Q intersect to each other at a point R. Prove that ∠PRQ=90∘.
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OC
View SolutionIn a parallelogram ABCD, bisectors of consecutive angles A and B intersect at P. Find the measure of ∠APB :
View Solution