If the angle between two radii of a circle be130∘, then the angle between the tangents at the end of these radii is:
50∘
90∘
40∘
70∘
The correct Answer is:A
Step by step video, text & image solution for If the angle between two radii of a circle be130^@, then the angle between the tangents at the end of these radii is: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
A30∘B60∘C90∘D120∘If one angle of a triangle is 130∘ , then the angle between the bisectors of the other two angles is
A65∘B115∘C130∘D155∘If one of the angles of a triangle is 130∘ then the angle between the bisectors of the other two angles can be
A50∘B65∘C90∘D155∘
The angle between two tangents to a circle may be 0∘.
View SolutionIf we draw a tangents to a circle at a given point on it, when the centre of the circle is known, then the angle between the tangent and radius of the circle is
View Solution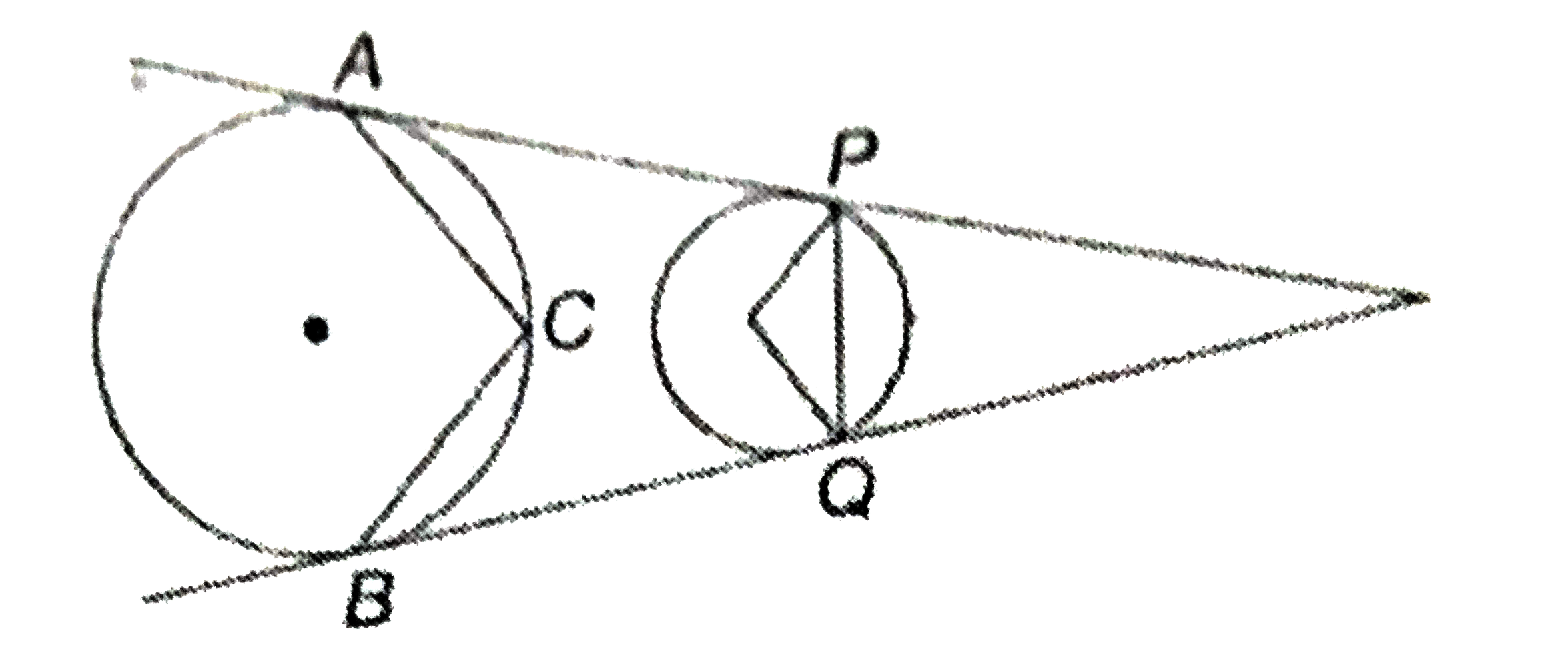
In the diagram above, A,B,P and Q are points of contacts of direct common tangents of the two circles. If ∠ACB is 120∘ , then find the angle between the two tangents and angle made by PQ at the centre of same circle.
View SolutionFind the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR=110∘
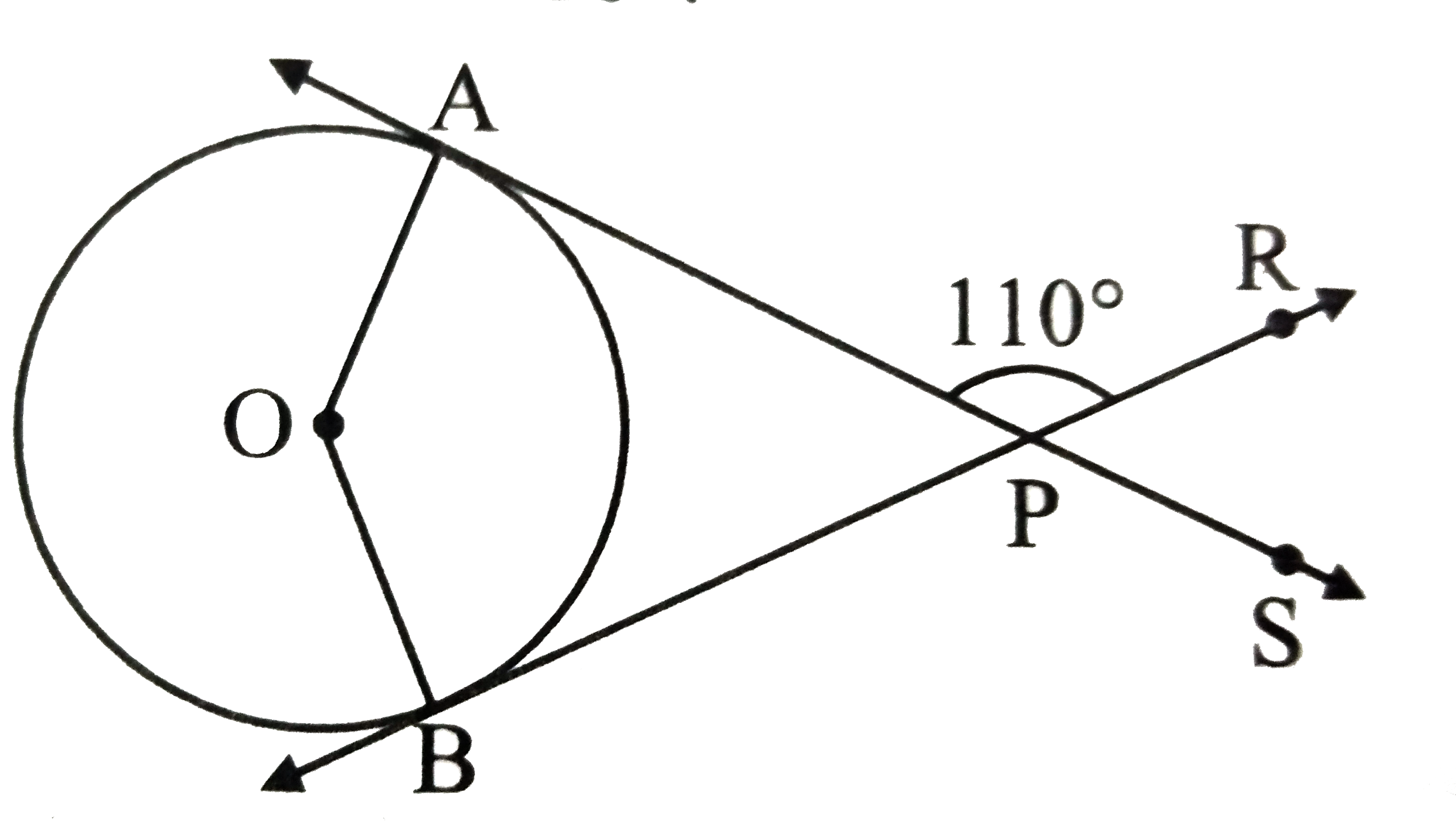
View SolutionIf one of the angles of a triangle is 130∘ , then the angle between the bisectors of the other two angles can be
View Solution