If angle between two radii of a circle is 80∘ , what will be the angle . between the tangents at the ends of the radii ?
The correct Answer is:100∘
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Identify the Given Information:
- We have a circle with center O.
- Two radii OA and OB are drawn, forming an angle of 80 degrees at the center (∠AOB = 80°).
2. Understanding the Geometry:
- When tangents are drawn from points A and B to the circle, they will meet at an external point P.
- The angles formed between the tangents and the radii can be analyzed.
3. Using Properties of Tangents:
- The angle between the two tangents (APB) can be found by using the property that the angle between the tangents from an external point is equal to the sum of the angles subtended by the radii at the center.
- Therefore, we need to find the angles AOP and BOP.
4. Finding Angles AOP and BOP:
- Since OA and OB are equal (both are radii), triangles AOP and BOP are congruent.
- Given that ∠AOB = 80°, we can divide this angle equally between the two angles AOP and BOP.
- Thus, ∠AOP = ∠BOP = 80° / 2 = 40°.
5. Finding Angles at Point P:
- The angle between the radius OA and the tangent AP is 90° (since the radius is perpendicular to the tangent at the point of contact).
- Therefore, ∠PAO = 90°.
6. Using Triangle Properties:
- In triangle AOP, the sum of angles is 180°.
- We have:
- ∠AOP = 40°
- ∠PAO = 90°
- Let ∠APO = x.
- Therefore, we can write the equation:
- 40° + 90° + x = 180°
- 130° + x = 180°
- x = 180° - 130° = 50°.
- So, ∠APO = 50°.
7. Finding the Angle APB:
- Since ∠APO = 50° and ∠BPO (which is equal to ∠APO due to symmetry) is also 50°,
- The angle between the tangents at points A and B is:
- ∠APB = ∠APO + ∠BPO = 50° + 50° = 100°.
Final Answer:
The angle between the tangents at the ends of the radii is 100 degrees.
---
- We have a circle with center O.
- Two radii OA and OB are drawn, forming an angle of 80 degrees at the center (∠AOB = 80°).
- When tangents are drawn from points A and B to the circle, they will meet at an external point P.
- The angles formed between the tangents and the radii can be analyzed.
- The angle between the two tangents (APB) can be found by using the property that the angle between the tangents from an external point is equal to the sum of the angles subtended by the radii at the center.
- Therefore, we need to find the angles AOP and BOP.
- Since OA and OB are equal (both are radii), triangles AOP and BOP are congruent.
- Given that ∠AOB = 80°, we can divide this angle equally between the two angles AOP and BOP.
- Thus, ∠AOP = ∠BOP = 80° / 2 = 40°.
- The angle between the radius OA and the tangent AP is 90° (since the radius is perpendicular to the tangent at the point of contact).
- Therefore, ∠PAO = 90°.
- In triangle AOP, the sum of angles is 180°.
- We have:
- ∠AOP = 40°
- ∠PAO = 90°
- Let ∠APO = x.
- Therefore, we can write the equation:
- 40° + 90° + x = 180°
- 130° + x = 180°
- x = 180° - 130° = 50°.
- So, ∠APO = 50°.
- Since ∠APO = 50° and ∠BPO (which is equal to ∠APO due to symmetry) is also 50°,
- The angle between the tangents at points A and B is:
- ∠APB = ∠APO + ∠BPO = 50° + 50° = 100°.
The angle between the tangents at the ends of the radii is 100 degrees.
Topper's Solved these Questions
- CIRCLES Book:VK GLOBAL PUBLICATIONChapter:CIRCLES Exercise:PROFICIENCY EXERCISE (Short Answer Questions - I 2 mark)
Explore 13 Videos
- CIRCLES Book:VK GLOBAL PUBLICATIONChapter:CIRCLES Exercise:PROFICIENCY EXERCISE (Short Answer Questions - II 3 mark)
Explore 22 Videos
- CIRCLES Book:VK GLOBAL PUBLICATIONChapter:CIRCLES Exercise:HOTS (Higher Order Thinking Skills)
Explore 4 Videos
- ARITHMETIC PROGRESSIONS Book:VK GLOBAL PUBLICATIONChapter:ARITHMETIC PROGRESSIONS Exercise:SELF ASSESSMENT TEST
Explore 10 Videos
- COORDINATE GEOMETRY Book:VK GLOBAL PUBLICATIONChapter:COORDINATE GEOMETRY Exercise:SELF-ASSESSMENT TEST
Explore 10 Videos
Similar Questions
If the angle between two radii of a circle is 130∘ then the angle between the tangents at the ends of the radii is
View SolutionIf the angle between two radii of a circle be130∘, then the angle between the tangents at the end of these radii is:
यदि किसी वृत्त की दो त्रिज्या के बीच का कोण 130∘ है, तो इन त्रिज्या के अंत में स्पर्शरेखाओं के बीच का कोण है
View Solution
Knowledge Check
The ratio between the area of two circles is 4:7. What will be the ratio of their radii ?
A2:√7B4:7C16:49D4:√7If a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
A30∘B60∘C90∘D120∘What is the maximum number of common tangents which can be drawn to the circle, if the distance between the circles is equal to the sum of their radii?
A0B1C3D4
The angle between two tangents to a circle may be 0∘.
View SolutionIf we draw a tangents to a circle at a given point on it, when the centre of the circle is known, then the angle between the tangent and radius of the circle is
View SolutionFind the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR=110∘
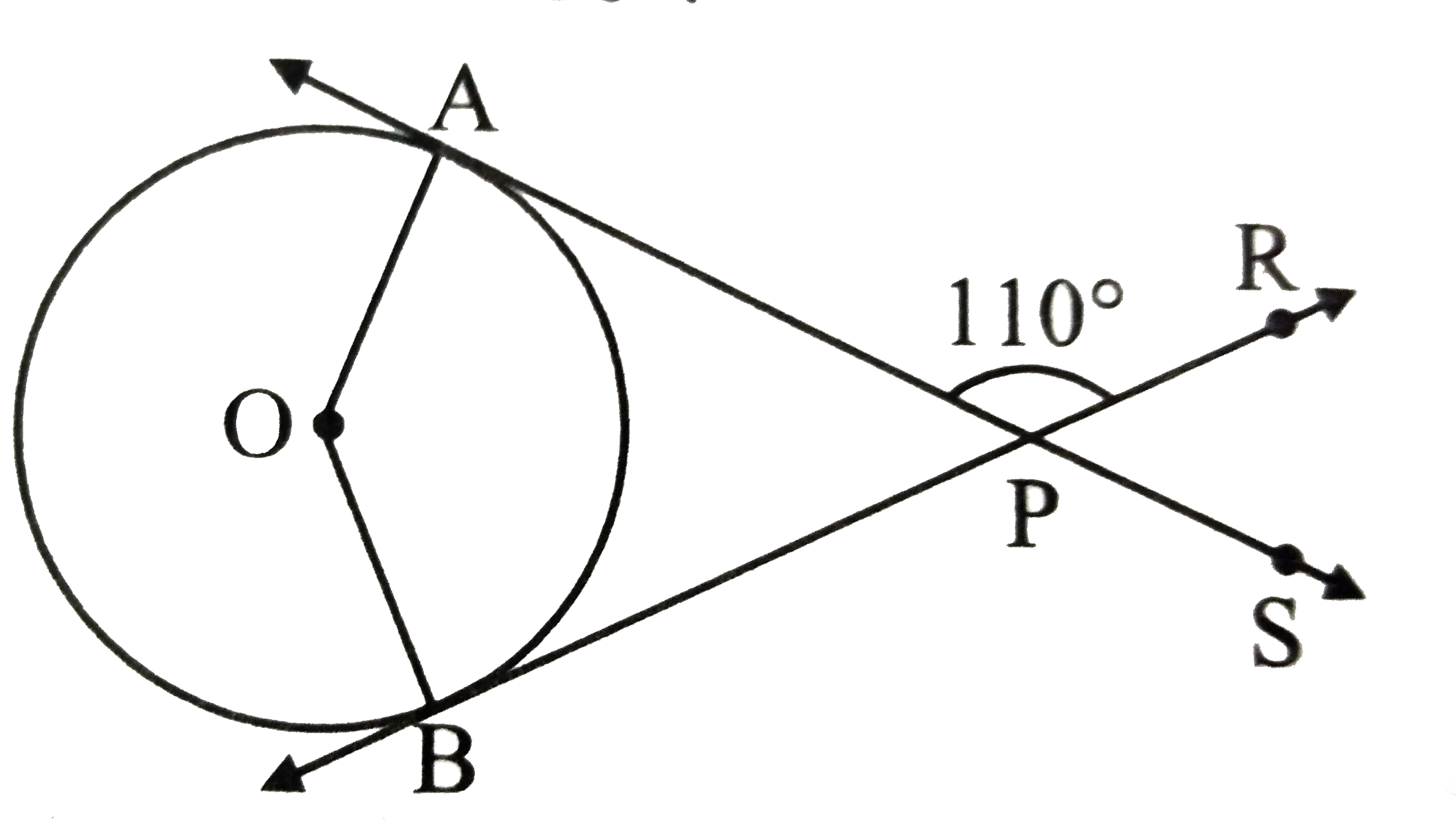
View SolutionIf a chord PQ subtends an angle of 80∘ at the centre of a circle, then angle between the tangents at P and Q is also 80∘
State true or false
View Solution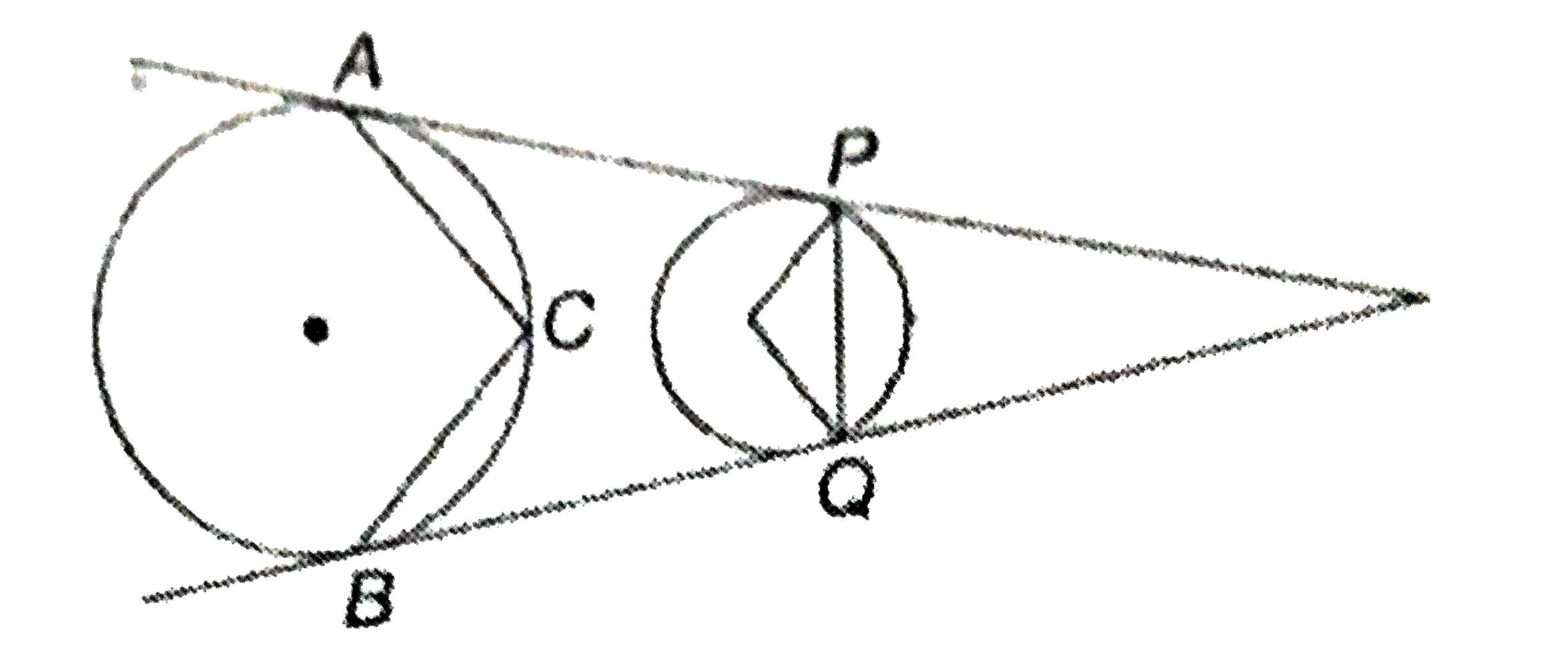
In the diagram above, A,B,P and Q are points of contacts of direct common tangents of the two circles. If ∠ACB is 120∘ , then find the angle between the two tangents and angle made by PQ at the centre of same circle.
View Solution

