In a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
(πBr2ω)28R
πBrω28R
(πBrω)28R
0
The correct Answer is:B
The flux linked with coil (made of wire of radius r) of area A and magnetic field B, is given by
ϕ=BAcosθ=B(πr22)cosωt
ϕ=πBr22cosωt [∵A=πr22 andθ=ωt]
By Faraday’s law of electromagnetic induction, induced emf, e=−dϕdt
Hence after differentiating
e=−ddt(πBr22 cos ωt)=πBr2ω2sinωt
(where, R = resistance in the circuit)
∴ Power P =e2R=π2B2r4ω2sin2ωt4R
∴ Mean power ¯¯¯P=π2B2r4ω24R.¯¯¯¯¯¯¯¯¯¯¯sin2ωt
=π2B2r4ω24R.12[∵¯¯¯¯¯¯¯¯¯¯¯sin2ωt=12]
=(πBr2ω)28R
Topper's Solved these Questions
Similar Questions
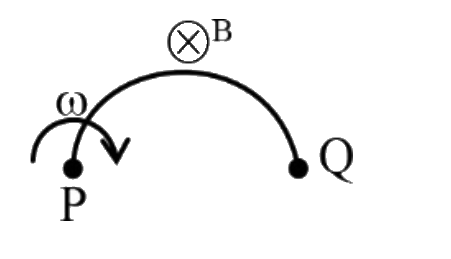
A wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
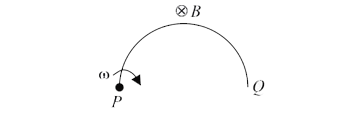
View SolutionA wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity ω . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then -
View Solution
Knowledge Check
In a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
A(πBr2ω)28RBπBrω28RC(πBrω)28RD0A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
AMω2LBMω2L8CMω2L4DMω2L2
A circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View SolutionCalculate the work that has to be done to stop an iron sphere of radius R rotating about its diameter with an angular velocity ω.
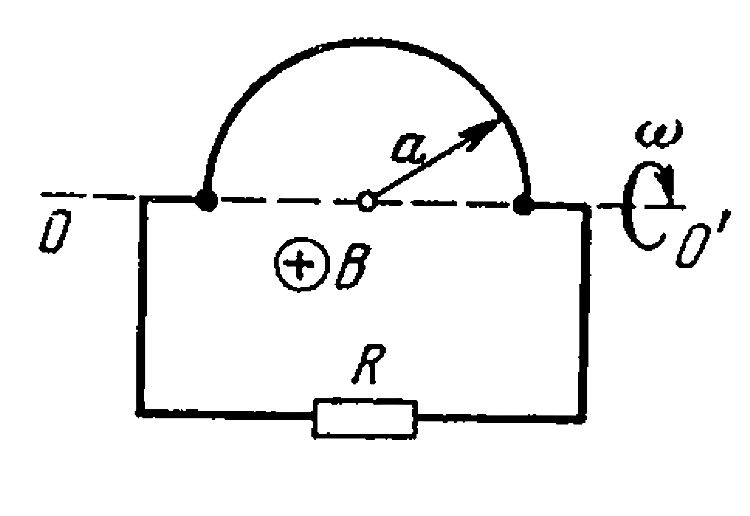
View SolutionA wire shaped as a semi-circle of radius a rotates about sn sxis OO' with an angular velocity ω in a unifrom magnetic field of induction B' (Fig). The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to R. NEglecting the magnetic field of the induced current, find the meand amount of thermal power being generated in the loop fueing a rotation period.
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA rectangular coil of single trun, having area A , rotates in a uniform magnetic field B with an angular velocity ω about an axis prependicular to the field. If initially the plane of the coil is perpendicular to the field, then the average induced emf when it has rotate through 90∘ is
View Solution