Suppose population A has 100 observations101,102,...,200and another population B has 100 observatons 151 , 152,...,250. If VAandVB represent the variances of the two populations respectively, then VAVB is
94
49
23
1
The correct Answer is:D
To solve the problem, we need to calculate the variances of populations A and B and then find the ratio of these variances.
Step 1: Define the populations
Population A consists of the observations from 101 to 200.
Population B consists of the observations from 151 to 250.
Step 2: Calculate the mean of each population
Mean of Population A (μ_A):
μA=Sum of observations in ANumber of observations in A=101+102+...+200100
The sum of an arithmetic series can be calculated using the formula:
Sum=n2×(first term+last term)
For Population A:
SumA=1002×(101+200)=50×301=15050
Thus,
μA=15050100=150.5
Mean of Population B (μ_B):
μB=151+152+...+250100
For Population B:
SumB=1002×(151+250)=50×401=20050
Thus,
μB=20050100=200.5
Step 3: Calculate the variance of each population
Variance of Population A (V_A):
VA=∑(xi−μA)2n
Where xi are the observations in Population A. We can also use the formula:
VA=∑x2in−μ2A
First, we need to calculate ∑x2i:
200∑i=101i2=n6(2a+(n−1)d)(2a+(n−1)d)=1006(2×101+99×1)(2×101+99×1)=1006(202+99)(202+99)=1006(301)(301)
Calculating ∑x2i:
200∑i=101i2=1006×3012=100×906016=1510166.67
Now calculate variance:
VA=1510166.67100−(150.5)2=15101.67−22650.25=−7548.58
Variance of Population B (V_B):
Using the same method:
VB=∑x2in−μ2B
Calculating ∑x2i for B:
250∑i=151i2=1006(2×151+99)(2×151+99)=1006(302+99)(302+99)=1006(401)(401)
Calculating ∑x2i:
250∑i=151i2=1006×4012=100×1608016=2680016.67
Now calculate variance:
VB=2680016.67100−(200.5)2=26800.17−40200.25=−13400.08
Step 4: Calculate the ratio of the variances
Now we can find the ratio of the variances:
VAVB=−7548.58−13400.08≈0.562
Final Answer
VAVB≈0.562
Population B consists of the observations from 151 to 250.
μA=Sum of observations in ANumber of observations in A=101+102+...+200100
The sum of an arithmetic series can be calculated using the formula:
Sum=n2×(first term+last term)
For Population A:
SumA=1002×(101+200)=50×301=15050
Thus,
μA=15050100=150.5
μB=151+152+...+250100
For Population B:
SumB=1002×(151+250)=50×401=20050
Thus,
μB=20050100=200.5
VA=∑(xi−μA)2n
Where xi are the observations in Population A. We can also use the formula:
VA=∑x2in−μ2A
First, we need to calculate ∑x2i:
200∑i=101i2=n6(2a+(n−1)d)(2a+(n−1)d)=1006(2×101+99×1)(2×101+99×1)=1006(202+99)(202+99)=1006(301)(301)
Calculating ∑x2i:
200∑i=101i2=1006×3012=100×906016=1510166.67
Now calculate variance:
VA=1510166.67100−(150.5)2=15101.67−22650.25=−7548.58
Using the same method:
VB=∑x2in−μ2B
Calculating ∑x2i for B:
250∑i=151i2=1006(2×151+99)(2×151+99)=1006(302+99)(302+99)=1006(401)(401)
Calculating ∑x2i:
250∑i=151i2=1006×4012=100×1608016=2680016.67
Now calculate variance:
VB=2680016.67100−(200.5)2=26800.17−40200.25=−13400.08
VAVB=−7548.58−13400.08≈0.562
VAVB≈0.562
Topper's Solved these Questions
Similar Questions
Suppose a population A has 100 observations 101,102,................,200 and another population B has 100 observations 151,152,........250. If VAandVB represent the variances of the two populations respectively,then VAVB is (a) 1 (b) 94 (c) 49 (d) 23
View SolutionIF VAandVB are the input voltages (either 5 V or 0 V) and Vo is the output voltage then the two gates represented in the following circuits (A) and (B) are :
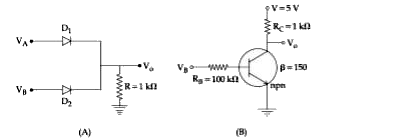
View Solution
Knowledge Check
Suppose a population A has 100 observations 101, 102,….,200 and another population B has 100 observations 151,152,….250. If VAand VB represent the variances of the two populations respectively, then VAVB is equal to
A1B9/4C4/9D2/3If the standard deviation of a populations is 10, what would be the population variance?
A 100 B. 30 C 5 D 20AA)100BB)30CC)5DD)20Two particles of mass mA and mB and their velocities are VA and VB respectively collides. After collision they interchanges their velocities, then ratio of mAmB is
AvAvBBvBvACvA+vBvB−vAD1
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
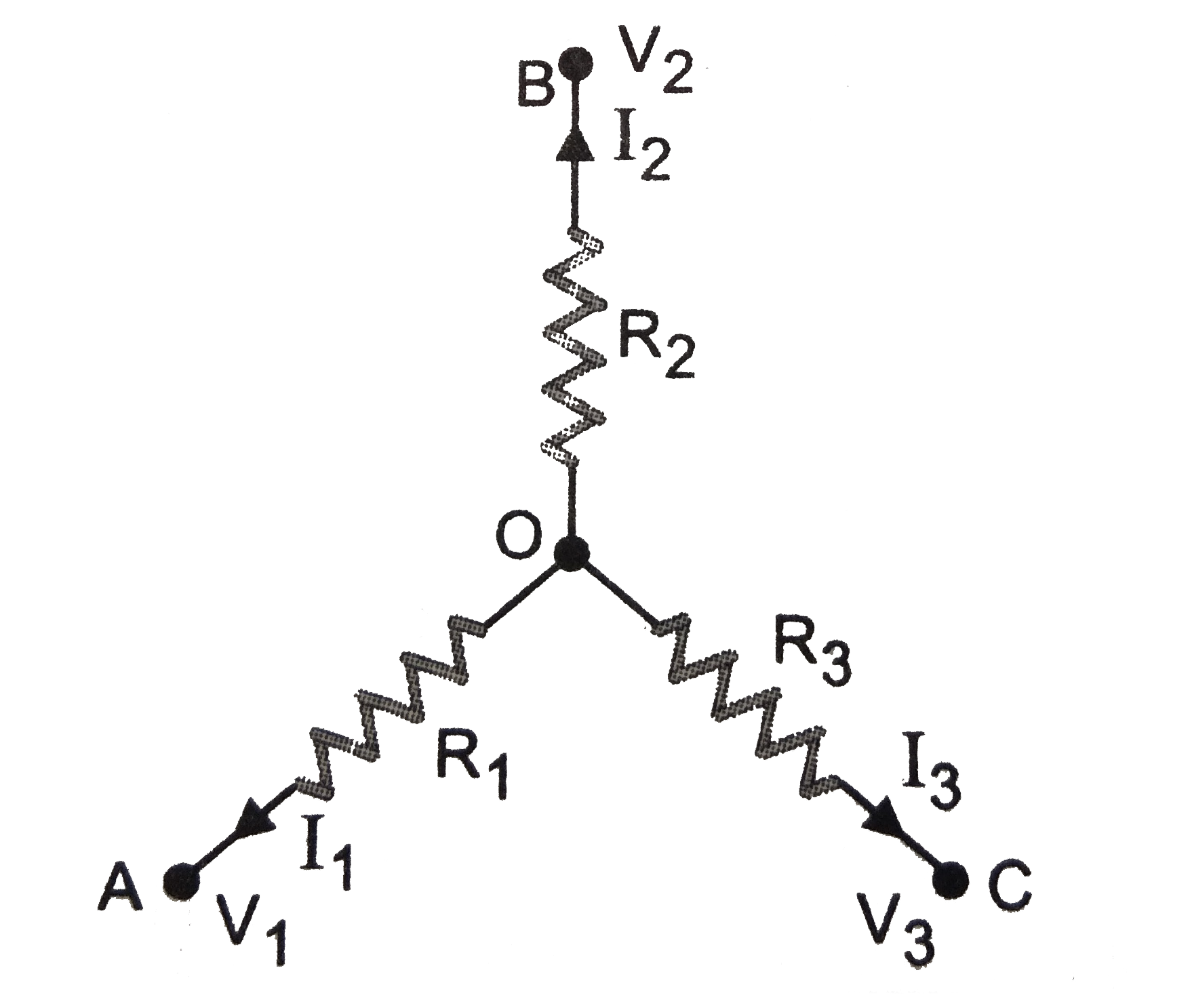
View SolutionTwo electric lamps A and B marked 220 V, 100 W and 220 V, 60 W respectively. Which of the two lamps has higher resistance ?
View SolutionPlanet A has massa M and radius R. Planet B has half the mass and half the radius of Planet A.If the escape velocities from the Planets A and B are vAandvB, respectively , then vAvB=n4. The vlaue of n is :
View SolutionTwo planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity vAvB is
View SolutionTwo elements A and B with atomic numbers ZA and ZB are used to produce charateristic X-rays with frequencies vA and vB respectively. If ZA:ZB=1:2, then vA:vB will be
View Solution

