Instruction : Answer the questions given below on the basis following figure.
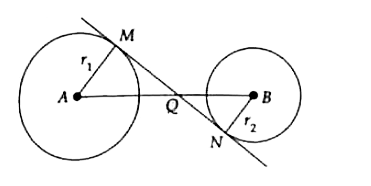
MN is a transverse common tangent. A and B are centres of the circles whose radii are respectively r1andr2. Length of AB is d.
Length of MN is
√d2−(r1+r2)2
√d2−(r1−r2)2
√d2+(r1+r2)2
√d2+(r1+r2)2
The correct Answer is:A
Step by step video, text & image solution for Instruction : Answer the questions given below on the basis following figure. MN is a transverse common tangent. A and B are centres of the circles whose radii are respectively r_1 and r_2. Length of AB is d. Length of MN is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B
8 Videos
Similar Questions
Instruction : Answer the questions given below on the basis following figure.
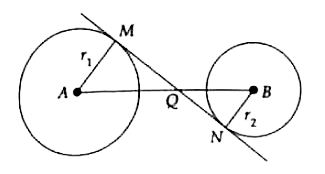
MN is a transverse common tangent. A and B are centres of the circles whose radii are respectively r1andr2. Length of AB is d.
Distance between point Q and N is
View SolutionInstruction : Answer the questions given below on the basis following figure.
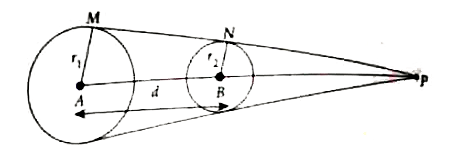
A and B are centres of the circles whose radii are respectively r1andr2 PNM is a direct common tangent touching the circles respectively at M and N.
Length of MN is
View Solution
Knowledge Check
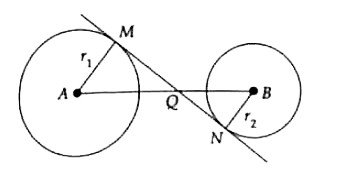
Instruction : Answer the questions given below on the basis following figure.
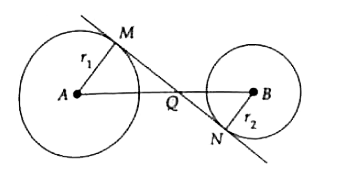
MN is a transverse common tangent. A and B are centres of the circles whose radii are respectively r1andr2. Length of AB is d.
Length of AQ isA1. r1dr1−r2B2. r2dr1−r2C3. r1dr1+r2D4. r2dr1+r2Instruction : Answer the questions given below on the basis following figure.
MN is a transverse common tangent. A and B are centres of the circles whose radii are respectively r1andr2. Length of AB is d.
Length of BQ isA1. r1dr1−r2B2. r2dr1−r2C3. r1dr1+r2D4. r2dr1+r2Instruction : Answer the questions given below on the basis following figure.
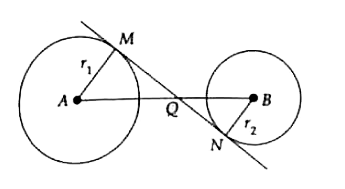
MN is a transverse common tangent. A and B are centres of the circles whose radii are respectively r1andr2. Length of AB is d.
Distance between point Q and M isAr1r1+r2√d2−(r1+r2)2Br2r1+r2√d2−(r1+r2)2Cr1r1−r2√d2−(r1−r2)2Dr2r1−r2√d2−(r1−r2)2
The length of the direct common tangent of two circles of radii 2 cm and 8 cm is 8 cm. Then the distance between the centres of the circles is
View SolutionIn the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
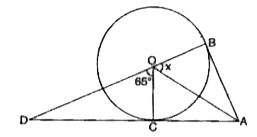
View SolutionSR is dirrect common tangent of two circles whose radii are respectively 8 cm and 3 cm and centres are 13 cm apart. If S and R are points of contact, then the length of SR is
View SolutionIn the given figure ,PR and ST are perpendiculars to tan- gent QR, PQ passes through centre O of the circle whose diameter is 10 cm . If PR = 9 cm what is the length (in cm.) of ST ?
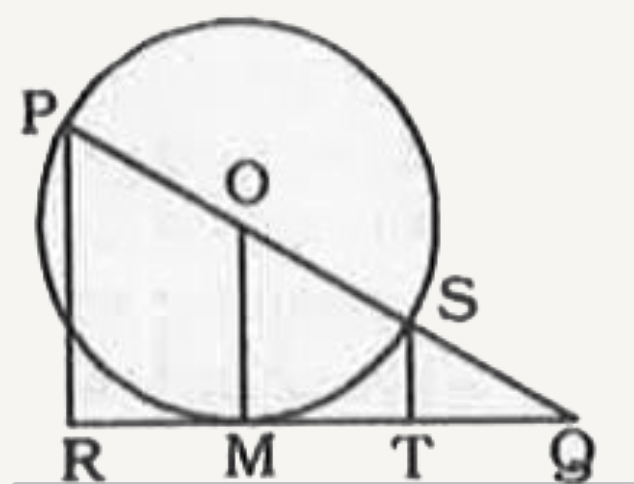
View SolutionIn the given figure ,PR and ST are perpendiculars to tan- gent QR, PQ passes through centre O of the circle whose diameter is 10 cm . If PR = 9 cm what is the length (in cm.) of ST ?

View Solution
