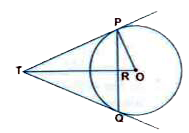
A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
ar√r2−a2
2ar√r2−a2
r2+a2√r2−a2
arr−a
The correct Answer is:A
To find the length of TP where T is the intersection of the tangents drawn at points P and Q on a circle with radius r and chord PQ of length 2a, we can follow these steps:
Step 1: Understand the Geometry
- The chord PQ has a length of 2a, which means that the distance from the center of the circle O to the midpoint M of the chord PQ can be found using the Pythagorean theorem.
- The radius r forms a right triangle with half the chord length a and the distance OM from the center to the chord.
Step 2: Calculate OM
Using the Pythagorean theorem:
OM2+a2=r2
Thus,
OM=√r2−a2
Step 3: Analyze the Tangents
- The tangents TP and TQ are equal in length because they are drawn from the same external point T to points P and Q.
- The angle between the line OT (from the center to point T) and the tangent line TP is 90∘.
Step 4: Use Similar Triangles
- In triangle OPT (where O is the center, P is on the circle, and T is the point where tangents meet), we can use the properties of similar triangles.
- The triangles OPT and OMT are similar because they share angle O and both have a right angle.
Step 5: Set Up Ratios
From the similarity of triangles, we can set up the ratio:
OTOM=OPOP
Where:
- OT=TP
- OM=√r2−a2
- OP=r
Thus, we can express TP:
TP√r2−a2=rTP
Step 6: Solve for TP
Cross-multiplying gives:
TP2=r⋅√r2−a2
Taking the square root:
TP=r2√r2−a2
Final Answer
The length of TP is:
TP=r2√r2−a2
- The chord PQ has a length of 2a, which means that the distance from the center of the circle O to the midpoint M of the chord PQ can be found using the Pythagorean theorem.
- The radius r forms a right triangle with half the chord length a and the distance OM from the center to the chord.
Using the Pythagorean theorem:
OM2+a2=r2
Thus,
OM=√r2−a2
- The tangents TP and TQ are equal in length because they are drawn from the same external point T to points P and Q.
- The angle between the line OT (from the center to point T) and the tangent line TP is 90∘.
- In triangle OPT (where O is the center, P is on the circle, and T is the point where tangents meet), we can use the properties of similar triangles.
- The triangles OPT and OMT are similar because they share angle O and both have a right angle.
From the similarity of triangles, we can set up the ratio:
OTOM=OPOP
Where:
- OT=TP
- OM=√r2−a2
- OP=r
TP√r2−a2=rTP
Cross-multiplying gives:
TP2=r⋅√r2−a2
Taking the square root:
TP=r2√r2−a2
The length of TP is:
TP=r2√r2−a2
Topper's Solved these Questions
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- CONGRUENCE AND SIMILAR TRIANGLES BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B
8 Videos
Similar Questions
Knowledge Check
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A163 cmB203 cmC185 cmD196 cm
The lengths of tangents drawn from an external point to a circle are ________.
View SolutionIn Fig , PQ is a chord of length 16 cm, of a radius 10 cm . The tangents at P and Q intersect at a point T. Find the length of TP.
View SolutionDraw a circle of radius 2.7 cm and draw chord PQ of length 4.5 cm. Draw tangents at P and Q without using centre.
View SolutionPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View Solution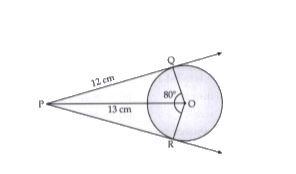
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the length of OR.
View Solution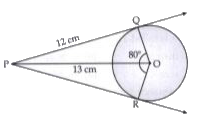
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the length of PR.
View Solution
