Calculate the wavelength of light used in an interference experiment from the following data: Fringe width = 0.03 cm. Distance between slits and eyepiece through which the interference pattern is observed is 1 m. Distance between the images of the virtural when a convex lens of focal length 16 cm is used at a distance of 80 cm from the eyepiece is 0.8 cm.
0.0006 Å
0.0006 m
600 cm
6000 Å
The correct Answer is:D
Step by step video, text & image solution for Calculate the wavelength of light used in an interference experiment from the following data: Fringe width = 0.03 cm. Distance between slits and eyepiece through which the interference pattern is observed is 1 m. Distance between the images of the virtural when a convex lens of focal length 16 cm is used at a distance of 80 cm from the eyepiece is 0.8 cm. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Calculate the wavelength of light used in an interference experiment from the following data: Fringe width = 0.03 cm. Distance between slits and eyepiece through which the interference pattern is observed is 1 m. Distance between the images of the virtural when a convex lens of focal length 16 cm is used at a distance of 80 cm from the eyepiece is 0.8 cm.
A0.0006 ÅB0.0006 mC600 cmD6000 ÅIn Young's double slit experiement, if L is the distance between the slits and the screen upon which interference pattern is observed, x is the average distance between the adjacent fringes and d being the slit separation. The wavelength of light if given by
A(a) xdLB(b) xLdC(c) LdxD(d) 1LdxAn object is placed at a distance of 20 cm from a convex lens of focal length 10 cm . The image is formed on the other side of the lens at a distance
A20 cmB10 cmC40 cmD30 cm
An object of length 2.0 cm is placed perpedicular to the principal axis of a conve lens of focal length 12 cm. Find the size of the image of the object is at a distance of 8.0 cm from the lens.
View SolutionIn a double slit interference experiment, the distance between the slits is 0.05 cm and screen is 2m away from the slits. The wavelength of light is 8.0×10−5 cm. The distance between successive fringes is
View SolutionIn Young's experiment, the distance between the slits is 0.025 cm and the distance of the screen from the slits is 100 cm. If two distance between their second maxima in cm is
View SolutionThe figure shows the interference pattern obtained in a double-slit experiment using light of wavelength 600 nm.
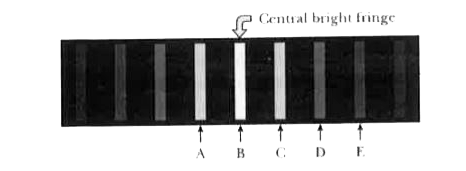
Which fringe is the same distance from both slits?
View SolutionA fringe width of a certain interference pattern is β=0.002 cm What is the distance of 5th dark fringe centre?
View Solution

