AB : zy : : CD : ?
WX
UV
XW
VU
The correct Answer is:C
Topper's Solved these Questions
- ANALOGY OR SIMILARITY Book:KIRAN PUBLICATIONChapter:ANALOGY OR SIMILARITY Exercise:TYPE-V
Explore 37 Videos
- ANALOGY OR SIMILARITY Book:KIRAN PUBLICATIONChapter:ANALOGY OR SIMILARITY Exercise:TYPE-IV
Explore 198 Videos
- ARRANGEMENT OF WORDS IN LOGICAL ORDER Book:KIRAN PUBLICATIONChapter:ARRANGEMENT OF WORDS IN LOGICAL ORDER Exercise:TYPE II
Explore 199 Videos
Similar Questions
ABCD is a cyclic trapezium & ABII CD, AB is diameter. BC = 2cm, AB = 8 cm, CD = ?
View SolutionAB and CD are two chords of a circle where AB = 10 cm, CD = 24 cm and AB||CD. Distance between AB and CD is 17 cm. Find the radius of the circle. (The chords are located on opposite sides of the centre)
View Solution
Knowledge Check
There is certain numbers of toys in the box. They are divided into such a way that the person who gets 1/4 of the whole gets thrice of what the others get on an average. Find the number of people amongst whom the toys are distributed?
AA) 8BB) 10CC) 12DD) 9AB and CD are two chords of a circle such that AB = 10 cm, CD - 24 cm and AB||CD. If the distance between AB and CD is 17 cm. Then, the radius of the circle is equal to
A13B169C26DNone of theseAB and CD are two chords of a circle such that AB= 10 cm, CD = 24 cm and AB|| CD. The distance between AB and CD is 17 cm. Then, the radius of the circle is equal to
A13cmB169cmC26cmDnone of these
In a right-angled triangle ABC, ∠C=90∘ and CD is perpendicular to AB. If AB x CD = CA x CB, then 1CD2 is equal to:
View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionIn a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View SolutionIf AB = 4.8 cm and CD = 2.8 cm, construct a line segment whose length is AB-CD.
View SolutionIn a right angled ΔABC,∠C=90∘andCD is the perpendicular on the hypotenuse AB,AB=c,BC=a,AC=bandCD=p, then :
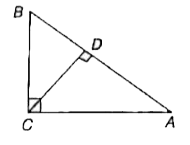
View Solution

