AB· : L:: BC:?
X
V
Y
W
The correct Answer is:D
Topper's Solved these Questions
- ANALOGY OR SIMILARITY Book:KIRAN PUBLICATIONChapter:ANALOGY OR SIMILARITY Exercise:TYPE-V
Explore 37 Videos
- ANALOGY OR SIMILARITY Book:KIRAN PUBLICATIONChapter:ANALOGY OR SIMILARITY Exercise:TYPE-IV
Explore 198 Videos
- ARRANGEMENT OF WORDS IN LOGICAL ORDER Book:KIRAN PUBLICATIONChapter:ARRANGEMENT OF WORDS IN LOGICAL ORDER Exercise:TYPE II
Explore 199 Videos
Similar Questions
ABC is a triangular frame made of a conducting wire and is right angled at B. Its side BC is vertical and AB is horizontal. The frame is placed in a uniform magnetic field B in vertically upward direction. The frame is rotated about its side BC with constant angular speed ω. Resistance of the entire frame is R. Neglect gravity. Length AB=L,BC=2L.
(a) Find the torque needed to keep the frame rotating with constant angular speed.
(b) Find the potential difference between points A and C.
View SolutionIn △ABC, AB:BC:DC=3:1:3
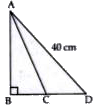
Find BC + CD
View Solution
Knowledge Check
In the diagram,AB:BC=1:3 and BC:CD: =5:2. The ratio AB:CD in the given diagram is
A0.12777777777778B0.12847222222222C0.2125DNone of theseThe ABC is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB,IBC and lCA are the moments of inertia of the plate about AB, BC and CA respectively. Which one of the following relation is correct?
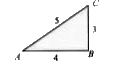 AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IAB
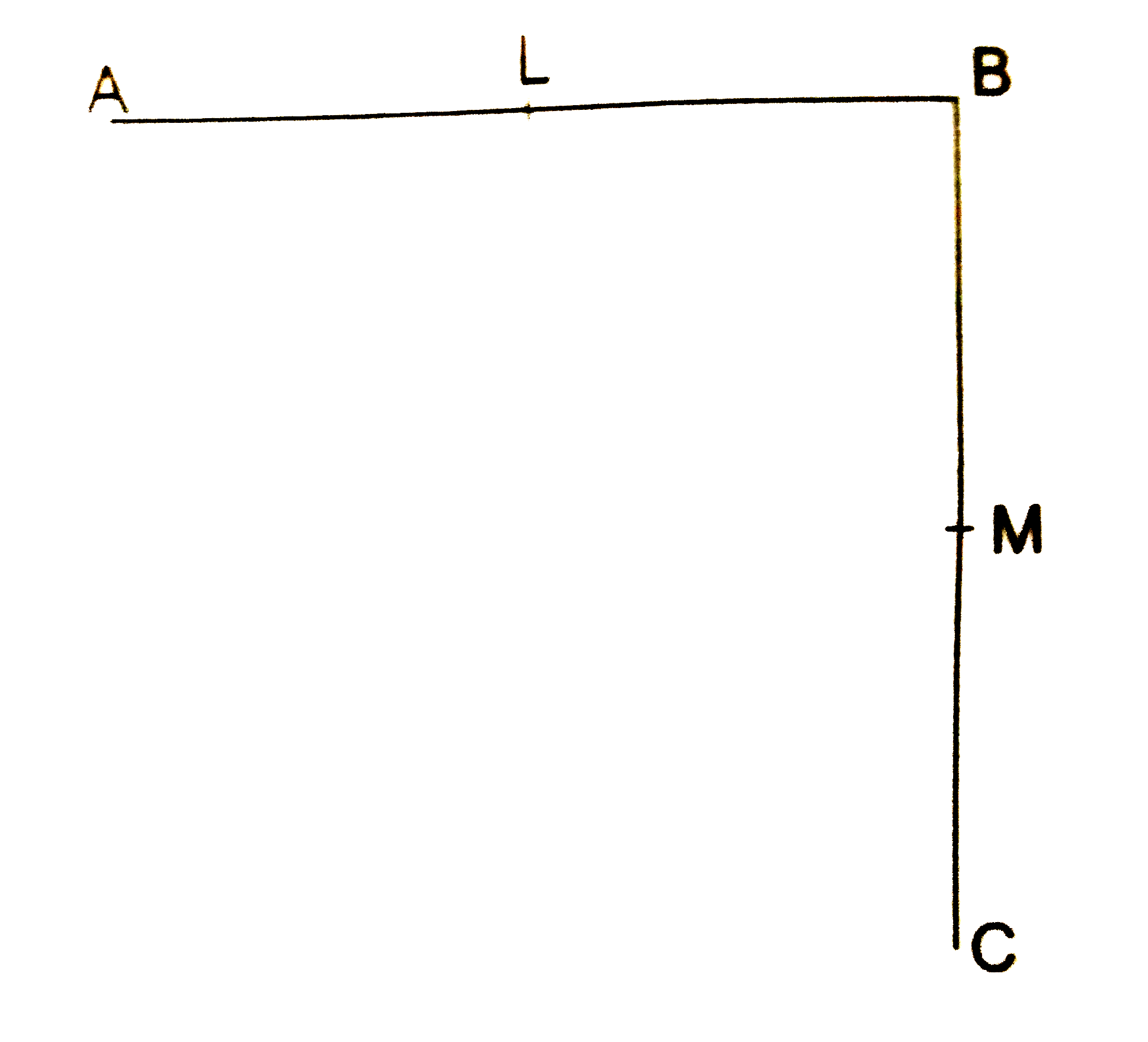
AIAB+IBC=ICABICA is maximumCIAB>IBCDIBC>IABL and M are the mid points of AB and BC respectively of ΔABC , right angled at B . 4LC2=
 AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these
AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these
In ΔABC,AB⊥BC and ∠ACB=30∘If AB=15m find BC
View SolutionA particle travels along the path ABC, as shown in the figure given below, AB = BC = l, calculate the path length and displacement of the particle
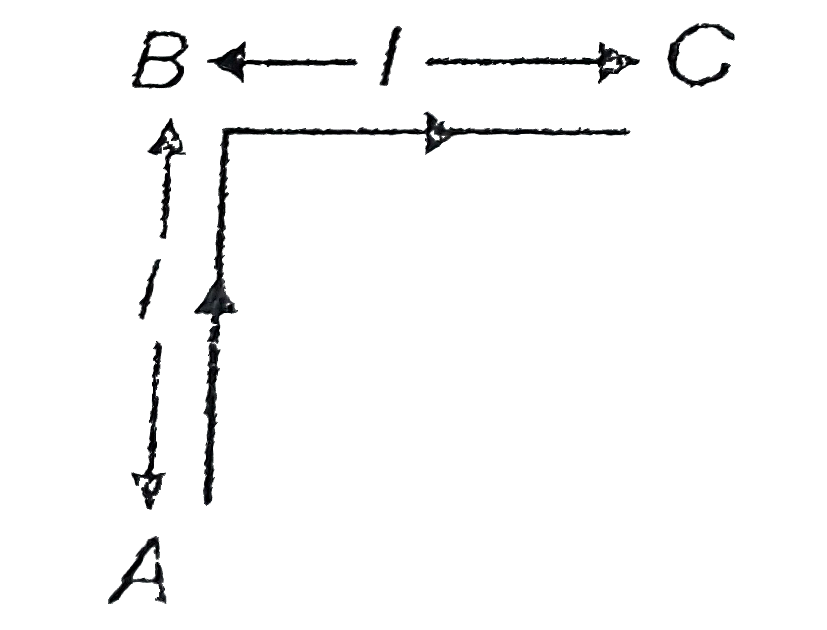
View SolutionIn the given figure L and M are the midpoints of AB and BC respectivcely
(i) If AB= BC prove that AL = MC
(ii) If BL = BM prove that AB=BC
View SolutionD is the midpoint of side BC of ΔABC. If AB=4, AC=6 and BC=8, then find l(AD) and hence perimeter of ΔABD.
View SolutionIn a triangle ABC,XandY are the points on ABandBC respectively. If BX=12ABandBY=12BCandAB=BC. Show that BX=BY.
View Solution

