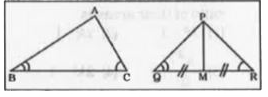
In ΔABC and ΔPQR,∠B=∠Q,∠C=∠R. M is the mid-point of side QR. If AB : PQ = 7 : 4, then
area (ΔABC)area (ΔPMR) is :
358
4916
498
3516
The correct Answer is:C
Step by step video & image solution for In Delta ABC and Delta PQR, angleB = angle Q, angleC = angle R. M is the mid-point of side QR. If AB : PQ = 7 : 4, then ("area " (Delta ABC))/("area " (Delta PMR)) is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - III
Explore 21 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - IV
Explore 169 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:Test Yourself
Explore 28 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
In a ΔABCPandQ are the mid-point or AB and AC, respectively. If O is the circume- centre of the ΔABC, then the value of (Area ofΔABCArea of ΔOPQ)cotBcotC equal to
View SolutionIn ΔABCandΔPQR,∠A=∠Qand∠B=∠R. Which side of ΔPQR should be equal to side AB of ΔABC, so that the two triangle are congruent ? Give reason for your answer.
View Solution
Knowledge Check
In ΔABCandΔPQR , If AB=AC, ∠C=∠P and ∠B=∠Q, then the two triangles are
Aisosceles but not congruentBisosceles and congruentCcongruent but not isoscelesDNeither congruent nor isoscelesIn ΔABC, if AB=AC and ∠B=50∘, then ∠C is equal to
A40∘B50∘C80∘D130∘ABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
A4:1B5:1C3:1Dcan't be determind
In ΔABCandΔPQR,∠A=∠Qand∠B=∠R. Which side of ΔPQRshould be equal to side BC of ΔABC ,so that the two triangle are congruent ? Give reason for your answere.
View SolutionIn ΔABC, P is a point on BC such that BP:PC=4:5 and Q is the mid - point of BP. Then area (ΔABQ) : area (ΔABC) is equal to :
View SolutionIf D,E and F are respectively the midpoint of the sides BC,CA and AB of a ΔABC and the area of ΔABC=36cm2 , then area of ΔDEF is -----
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View SolutionIn an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
View Solution
