A kite in the shape of a square with a diagonal 32 cm attached to an equilateral triagle of the base 8 cm. Approximately how much paper has been used to make it ? (Use √3=1.732)
539.712cm2
538.721cm2
540.712cm2
539.217cm2
The correct Answer is:A
To find the total area of the kite made of a square and an equilateral triangle, we will follow these steps:
Step 1: Calculate the area of the square
The area of a square can be calculated using the formula:
Area of square=12×diagonal2
Given the diagonal of the square is 32 cm, we substitute this value into the formula:
Area of square=12×(32)2=12×1024=512 cm2
Step 2: Calculate the area of the equilateral triangle
The area of an equilateral triangle can be calculated using the formula:
Area of triangle=√34×a2
where a is the length of the side of the triangle. Given that the base of the triangle is 8 cm, we can use this as the side length:
Area of triangle=√34×(8)2=√34×64=16√3 cm2
Now, substituting √3=1.732:
Area of triangle=16×1.732=27.712 cm2
Step 3: Calculate the total area
Now, we can find the total area of the kite by adding the area of the square and the area of the triangle:
Total area=Area of square+Area of triangle=512+27.712=539.712 cm2
Final Answer
Thus, the total area of paper used to make the kite is approximately:
539.712 cm2
---
The area of a square can be calculated using the formula:
Area of square=12×diagonal2
Given the diagonal of the square is 32 cm, we substitute this value into the formula:
Area of square=12×(32)2=12×1024=512 cm2
The area of an equilateral triangle can be calculated using the formula:
Area of triangle=√34×a2
where a is the length of the side of the triangle. Given that the base of the triangle is 8 cm, we can use this as the side length:
Area of triangle=√34×(8)2=√34×64=16√3 cm2
Now, substituting √3=1.732:
Area of triangle=16×1.732=27.712 cm2
Now, we can find the total area of the kite by adding the area of the square and the area of the triangle:
Total area=Area of square+Area of triangle=512+27.712=539.712 cm2
Thus, the total area of paper used to make the kite is approximately:
539.712 cm2
Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - III
Explore 21 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - IV
Explore 169 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:Test Yourself
Explore 28 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
A kite in the shape of a square with a diagonal 32cm and an isosceles triangle of base 8cm and sides 6cm each is to be made of three different shades as shown in Figure . How much paper of each shade has been used in it ?
View SolutionA kite in the shape of a square with a diagonal 32cm and an isosceles triangle of base 8cm and sides 6cm each is to be made of three different shades as shown in Figure. How much paper of each shade has been used in it?
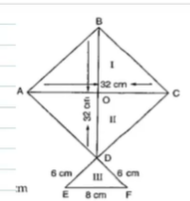
View Solution
Knowledge Check
If the diagonal of a square is (1.02)√2cm, then its approximate area is
A1.4cm2B1.04cm2C1.5cm2D1.7cm2The base of a right prism is an equilateral triangle of area 173cm2 and the volume of the prism is 10380cm3. The area of the lateral surface of the prism is (use √3=1.73)
A1200cm2B2400cm2C3600cm2D4380cm2
The height of an equilateral triangle measures 9 cm. Find its area, correct to 2 places of decimal. (Take √3=1.732.)
View SolutionIn the given figure, ΔPQR is an equilateral triangle of side 8cmP,Q,R are centres of circular arcs each of radius 4cm find the area of shaded region. (use π=3.14and√3=1.732)
View SolutionThe side of an equilateral triangle is 6√3 cm. Find the area of the triangle. [Take √3=1.732]
View SolutionThe base of a right pyramid is an equilateral triangle with side 8 cm, and the height of the pyramid is 24√3 cm. The volume (in cm3) of the pyramid is:
View SolutionFind the area of the shaded region in the given figure, where a circular of arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made. [ Use √3=1.73 and π=3.14]

View SolutionIn the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3=1.73 and π=3.14]
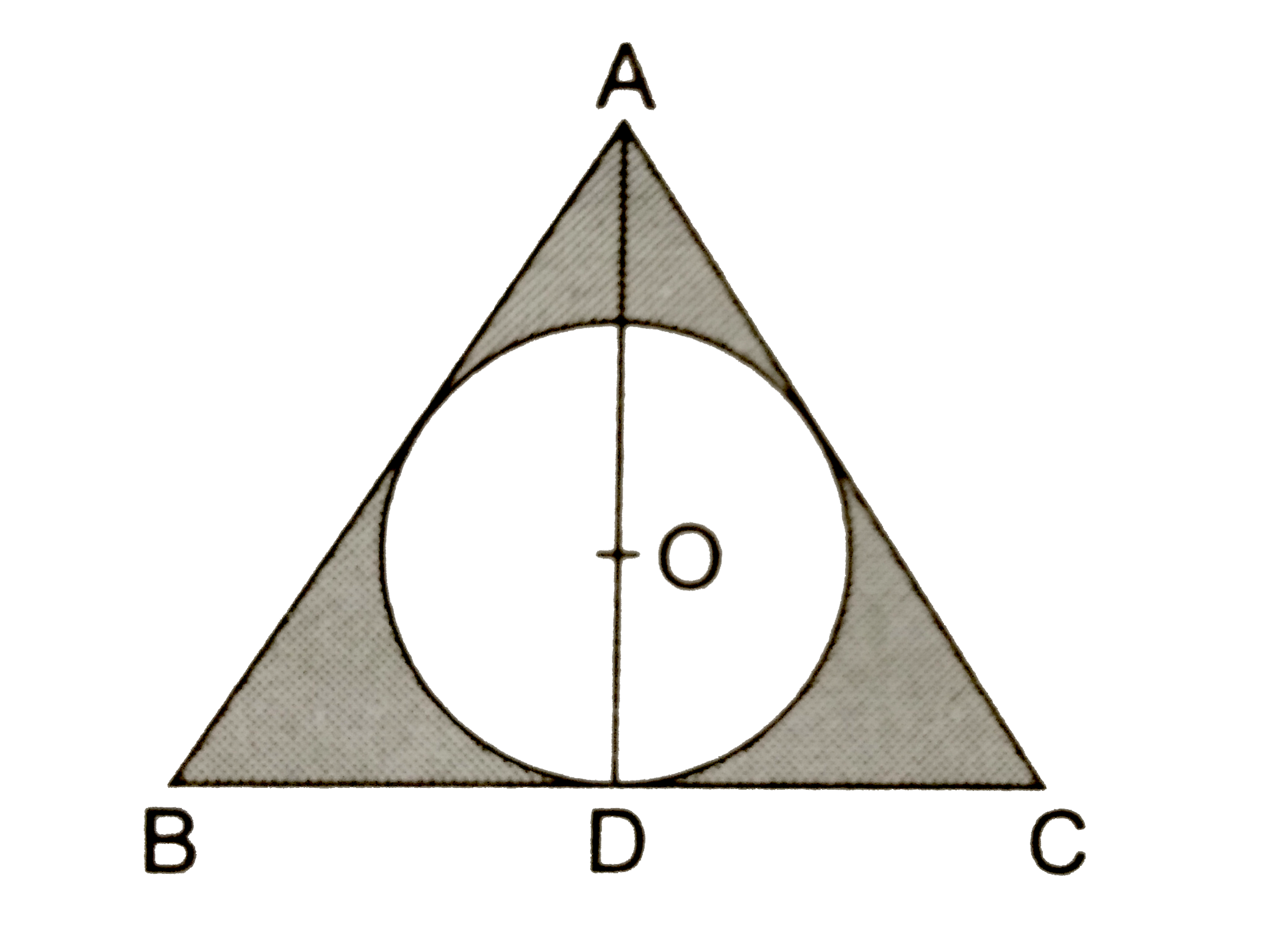
View Solution