Question

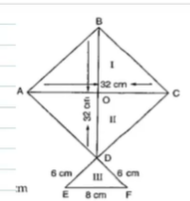
A kite in the shape of a square with a diagonal $32cm$ and an isosceles triangle of base $8cm$ and sides $6cm$ each is to be made of three different shades as shown in Figure . How much paper of each shade has been used in it ?

Explanation

To solve the problem, we need to find the areas of the kite and the isosceles triangle separately, and then determine how much paper of each shade has been used.

Step 1: Calculate the area of the square (kite)
The kite is in the shape of a square with a diagonal of 32 cm. The area \( A \) of a square can be calculated using the formula:

\( A = \frac{d^2}{2} \)

where \( d \) is the length of the diagonal.

Substituting the given value:

\( A = \frac{32^2}{2} = \frac{1024}{2} = 512 \text{ cm}^2 \)

Step 2: Calculate the area of the isosceles triangle
The isosceles triangle has a base of 8 cm and two equal sides of 6 cm each. To find the area of the triangle, we can use Heron's formula.

First, we need to calculate the semi-perimeter \( s \):

\( s = \frac{a + b + c}{2} = \frac{6 + 6 + 8}{2} = 10 \text{ cm} \)

Now, we can use Heron's formula to find the area \( A \):

\( A = \sqrt{s(s-a)(s-b)(s-c)} \)

Substituting the values:

\( A = \sqrt{10(10-6)(10-6)(10-8)} = \sqrt{10 \times 4 \times 4 \times 2} = \sqrt{80 \times 2} = \sqrt{160} = 4\sqrt{10} \text{ cm}^2 \)

Calculating \( 4\sqrt{10} \):

\( \sqrt{10} \approx 3.16 \Rightarrow 4\sqrt{10} \approx 4 \times 3.16 = 12.64 \text{ cm}^2 \)

Step 3: Total area of the kite and triangle
Now, we add the areas of the square and the triangle to find the total area:

\( \text{Total Area} = \text{Area of Square} + \text{Area of Triangle} = 512 + 12.64 = 524.64 \text{ cm}^2 \)

Step 4: Area of each shade
Assuming the kite is divided into three different shaded regions, we can distribute the areas accordingly. If we assume equal distribution among the three shades, each shade will cover:

\( \text{Area of each shade} = \frac{\text{Total Area}}{3} = \frac{524.64}{3} \approx 174.88 \text{ cm}^2 \)

Final Answer
- Area of the square (kite): \( 512 \text{ cm}^2 \)
- Area of the triangle: \( 12.64 \text{ cm}^2 \)
- Total area: \( 524.64 \text{ cm}^2 \)
- Area of each shade: \( \approx 174.88 \text{ cm}^2 \)