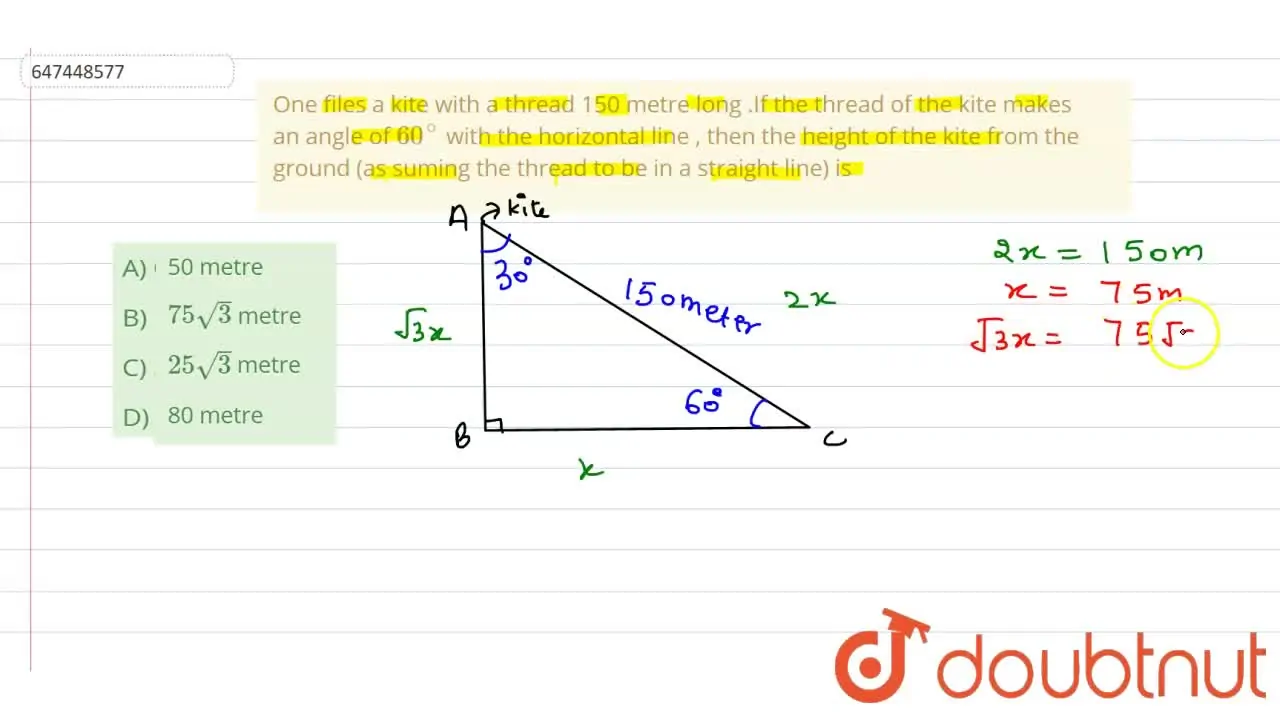
One files a kite with a thread 150 metre long .If the thread of the kite makes an angle of 60∘ with the horizontal line , then the height of the kite from the ground (as suming the thread to be in a straight line) is
50 metre
75√3 metre
25√3 metre
80 metre
The correct Answer is:B
Step by step video, text & image solution for One files a kite with a thread 150 metre long .If the thread of the kite makes an angle of 60^(@) with the horizontal line , then the height of the kite from the ground (as suming the thread to be in a straight line) is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
- BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -IV22videos
TRIGONOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE -V45videos
TRIGONOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - TRIGONOMETRY EXERCISE - TYPE - II420videos
TRIGONOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - TIME AND WORKEXERCISE - TEST YOURSELF25videos
TIME AND WORK
Similar Questions
A kite is flown with a thread of 250 m length. If the thread is assumed to be stretched and makes an angle of 60∘ with the horizontal, then the height of the kite above the ground is (approx.) :
View SolutionThe string of a kite is 150 m long and it makes an angle 60∘ with the horizontal. Find the height of the kite above the ground. (Assume string to be tight)
View SolutionThe string of a kite is 150 m long and it makes an angle 60∘ with the horizontal. Find the height of the kite above the ground. (Assume string to be tight)
View SolutionA flying kite make an angle of 30∘ with the floor. If string of kite is 100m, then height of kite is
View SolutionA kite is flying, attached to a thread which is 165m long. The thread makes an angle of 30∘ with the ground. Find the height of the kite from the ground , assuming that there is no slack in the thread.
View SolutionThe string of a kite is 250 m long and it makes an angle of 60∘ with the horizontal. Find the height of the kite is assuming that there is no slackness in the string.
View SolutionThe thread of a kite makes angle 60∘ with the horizontal plane . If the length of the thread be 80 m , then the vertical height of the kite will be
View SolutionThe string of a kite is 100 metres long and it makes an angle of 60o with the horizontal. Find the height of the kite, assuming that there is no slack in the string.
View SolutionA kite is flying at an inclination of 60∘ with the horizontal. If the length of the thread is 120 m, then the height of the kite is
View SolutionA kite is flying at a height of 50√3 m from the horizontal. It is attached with a string and makes an angle 60∘ with the horizontal. Find the length of the string.
View Solution