A kite is flying at a height of 50√3 m from the horizontal. It is attached with a string and makes an angle 60∘ with the horizontal. Find the length of the string.
The correct Answer is:100 m
To find the length of the string attached to the kite, we can use the properties of a right triangle formed by the height of the kite, the horizontal distance, and the string itself. Here’s the step-by-step solution:
Step 1: Understand the Problem
We know that the kite is flying at a height of 50√3 meters from the horizontal and makes an angle of 60∘ with the horizontal. We need to find the length of the string, which acts as the hypotenuse of the right triangle formed.
Step 2: Draw the Right Triangle
1. Draw a horizontal line to represent the ground.
2. From a point on this line, draw a vertical line up to a height of 50√3 meters. This represents the height of the kite.
3. Connect the top of this vertical line to the point on the horizontal line where the string is attached, forming a right triangle.
Step 3: Label the Triangle
- Let the point where the kite is located be point A (top of the vertical line).
- Let the point on the ground directly below the kite be point B.
- Let the point where the string is attached to the ground be point C.
- The height AB=50√3 m.
- The angle CAB=60∘.
- The length of the string AC is what we need to find.
Step 4: Use the Sine Function
In the right triangle ABC:
- The sine of angle C (which is 60∘) is given by the formula:
sin(C)=OppositeHypotenuse=ABAC
Here, AB is the height 50√3 m and AC is the length of the string x.
Step 5: Set Up the Equation
Substituting the known values into the sine formula:
sin(60∘)=50√3x
We know that sin(60∘)=√32.
Step 6: Solve for x
Substituting sin(60∘) into the equation:
√32=50√3x
Cross-multiplying gives:
√3⋅x=100√3
Dividing both sides by √3:
x=100
Final Answer
The length of the string is 100 meters.
---
We know that the kite is flying at a height of 50√3 meters from the horizontal and makes an angle of 60∘ with the horizontal. We need to find the length of the string, which acts as the hypotenuse of the right triangle formed.
1. Draw a horizontal line to represent the ground.
2. From a point on this line, draw a vertical line up to a height of 50√3 meters. This represents the height of the kite.
3. Connect the top of this vertical line to the point on the horizontal line where the string is attached, forming a right triangle.
- Let the point where the kite is located be point A (top of the vertical line).
- Let the point on the ground directly below the kite be point B.
- Let the point where the string is attached to the ground be point C.
- The height AB=50√3 m.
- The angle CAB=60∘.
- The length of the string AC is what we need to find.
In the right triangle ABC:
- The sine of angle C (which is 60∘) is given by the formula:
sin(C)=OppositeHypotenuse=ABAC
Here, AB is the height 50√3 m and AC is the length of the string x.
Substituting the known values into the sine formula:
sin(60∘)=50√3x
We know that sin(60∘)=√32.
Substituting sin(60∘) into the equation:
√32=50√3x
Cross-multiplying gives:
√3⋅x=100√3
Dividing both sides by √3:
x=100
The length of the string is 100 meters.
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
20 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - LONG ANSWER TYPE QUESTIONS
19 Videos
- REAL NUMBERSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTION
15 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Practice -Test
5 Videos
Similar Questions
A kite is flying at a height of 75 metres from the ground level, attached to a string inclined at 60o to the horizontal. Find the length of the string to the nearest metre.
View SolutionThe string of a kite is 150 m long and it makes an angle 60∘ with the horizontal. Find the height of the kite above the ground. (Assume string to be tight)
View Solution
Knowledge Check
A kite is flying at a height of 123 m. The thread attached to it is assumed to bestretched straight and makes an angle of 60 degree with the level ground. The length ofthe string is (nearest to a whole number):
A140 mB139 mC142 mD138 mA kite is flown with a thread of 250 m length. If the thread is assumed to be stretched and makes an angle of 60∘ with the horizontal, then the height of the kite above the ground is (approx.) :
A216.25 mB215.25 mC212.25 mD210.25 mThe string of a kite is 150 m long and it makes an angle 60∘ with the horizontal. Find the height of the kite above the ground. (Assume string to be tight)
A75 mB75√3 mC80 mD80√3m
A kite if flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground . If the length of the string is 40√3 . find the inclination of the string with the ground
View SolutionA body of mass mis suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
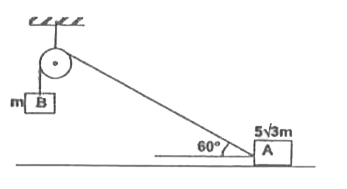
View SolutionA block A of mass 5√4m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
View SolutionA kite is flying at a height 80 m above the ground . The string of the kite which is temporarily attached to the ground makes an angle 45∘ with the ground. If there is no slack in the string, then the length of the string is
View SolutionA kite is flying at the height of 75 m from the ground .The string makes an angle θ (where cotθ=815) with the level ground .As - summing that there is no slack in the string the length of the string is equal to :
View Solution
