Which one of the following differential equations has a periodic solution ?
d2xdt2+μx=0
d2xdt2−μx=0
xdxdt+μt=0
dxdt+μxt=0
The correct Answer is:A
To determine which differential equation has a periodic solution, we can analyze the standard form of differential equations known to produce periodic solutions.
1. Understand the Concept of Periodic Solutions:
- A periodic solution is a function that repeats its values at regular intervals, typically described by sine or cosine functions. The simplest example of such a solution arises from the equations of Simple Harmonic Motion (SHM).
2. Identify the Standard Form of SHM:
- The standard differential equation for SHM is given by:
d2xdt2+μx=0
- Here, μ is a constant that relates to the stiffness of the system.
3. Solve the SHM Equation:
- The general solution to this differential equation can be expressed as:
x(t)=Acos(ωt−ϕ)orx(t)=Asin(ωt−ϕ)
- Where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
4. Recognize the Periodicity:
- Both forms of the solution (sine and cosine) are periodic functions with a period of T=2πω. This means that the function will repeat its values every T seconds.
5. Evaluate Given Options:
- If the question provides multiple differential equations, we would check each one to see if it can be transformed into the form of the SHM equation. The one that can be expressed in this form will have a periodic solution.
6. Conclusion:
- Based on the knowledge of SHM, the answer to the question is the differential equation that resembles the form d2xdt2+μx=0.
Final Answer:
- The differential equation that has a periodic solution is option A.
- A periodic solution is a function that repeats its values at regular intervals, typically described by sine or cosine functions. The simplest example of such a solution arises from the equations of Simple Harmonic Motion (SHM).
- The standard differential equation for SHM is given by:
d2xdt2+μx=0
- Here, μ is a constant that relates to the stiffness of the system.
- The general solution to this differential equation can be expressed as:
x(t)=Acos(ωt−ϕ)orx(t)=Asin(ωt−ϕ)
- Where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
- Both forms of the solution (sine and cosine) are periodic functions with a period of T=2πω. This means that the function will repeat its values every T seconds.
- If the question provides multiple differential equations, we would check each one to see if it can be transformed into the form of the SHM equation. The one that can be expressed in this form will have a periodic solution.
- Based on the knowledge of SHM, the answer to the question is the differential equation that resembles the form d2xdt2+μx=0.
- The differential equation that has a periodic solution is option A.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which one of the following differential equations has the general solution y=aex+be−x ?
Ad2ydx2+y=0Bd2ydx2−y=0Cd2ydx2+y=1Ddydx−y=0which one of the following differential equation is not linear ?
Ad2ydx2+4y=0Bxdydx+y=x3C(x−y)2dydx=9Dcos2xdydx+y=tanxWhich of the following differential equation is not degree 1
Ax3y2+(x+x2)y21+exy3=sinxBy1/22+sinxy1+xy=xC√y1+y=x+1Dy=2y1+√y1+y
Which one of the differential equation is not linear
View SolutionSolution of differential equation
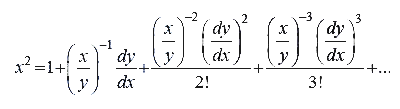
View SolutionWhich of the following differential equations has y = x as one of its particular solution?
View SolutionWhich of the following differential equation has the same order and degree?
View SolutionWhich one of the following differential equations represents the family of straight lines which are at unit distance from the origin ?
View Solution
