If the angle between the vectors →aand→b is π3. Then what is the angle between −5→aand6→b ?
π6
2π3
2π5
3π7
The correct Answer is:B
To find the angle between the vectors −5→a and 6→b given that the angle between →a and →b is π3, we can follow these steps:
Step 1: Understand the Given Information
We know that the angle between the vectors →a and →b is π3 radians, which is equivalent to 60∘.
Step 2: Analyze the Effect of Scalar Multiplication
When we multiply a vector by a scalar, the direction of the vector may change (if the scalar is negative), but the angle between the vectors remains unchanged. Therefore, the angle between →a and 6→b is still π3 (or 60∘).
Step 3: Determine the Angle Between −5→a and 6→b
The vector −5→a is in the opposite direction of 5→a. When we consider the angle between −5→a and 6→b, we can visualize it as follows:
- The angle between →a and →b is 60∘.
- The angle between −5→a and →b is 180∘−60∘=120∘.
Step 4: Convert the Angle to Radians
Now, we need to express 120∘ in radians:
120∘=120×π180=2π3
Conclusion
Thus, the angle between the vectors −5→a and 6→b is 2π3 radians.
We know that the angle between the vectors →a and →b is π3 radians, which is equivalent to 60∘.
When we multiply a vector by a scalar, the direction of the vector may change (if the scalar is negative), but the angle between the vectors remains unchanged. Therefore, the angle between →a and 6→b is still π3 (or 60∘).
The vector −5→a is in the opposite direction of 5→a. When we consider the angle between −5→a and 6→b, we can visualize it as follows:
- The angle between →a and →b is 60∘.
- The angle between −5→a and →b is 180∘−60∘=120∘.
Now, we need to express 120∘ in radians:
120∘=120×π180=2π3
Thus, the angle between the vectors −5→a and 6→b is 2π3 radians.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the angle between the vectors →aand→b is π3, what is the angle between −5→aand6→b?
Aπ6B2π3C2π5D3π7If the angle between the vectors →a and →b is an acute angle, then the diffrence →a−→b is
AThe major diagonal of the parallelogramBThe minor diagnol of the parallelogramCAny of the aboveDNone of the aboveWhat is the angle between the vector →A and →B as shown in figure ?
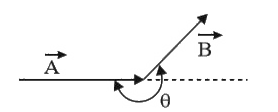 AθBπ−θCθ−πD2π−θ
AθBπ−θCθ−πD2π−θ
If θ be the angle between two vectors →a and →b, then →a.→b≥0 only when
View SolutionTwo vectors →a and →b are such that ∣∣→a+→b∣∣=∣∣→a−→b∣∣. What is the angle between →a and →b?
View SolutionThe angle between Vectors (→A×→B) and (→B×→A) is
View SolutionThe angle between vectors →Aand→B is 60∘ What is the ratio →A.→B and ∣∣→A×→B∣∣
View SolutionIf A=5 units,B=6 units and ∣∣→A×→B∣∣=15units, then what is the angle between →A and →B?
View Solution
