The angle between Vectors (→A×→B) and (→B×→A) is
Zero
π
π/4
π/2
The correct Answer is:B
To find the angle between the vectors →A×→B and →B×→A, we can follow these steps:
Step 1: Understand the Cross Product
The cross product of two vectors →A and →B is defined as:
→A×→B=|→A||→B|sin(θ)^n
where θ is the angle between the vectors →A and →B, and ^n is the unit vector perpendicular to the plane formed by →A and →B.
Step 2: Determine the Direction of the Cross Products
- The vector →A×→B is directed according to the right-hand rule and is perpendicular to the plane formed by →A and →B.
- The vector →B×→A is also directed according to the right-hand rule, but since the order of the vectors is reversed, it will point in the opposite direction. Thus, we can express it as:
→B×→A=−(→A×→B)
Step 3: Find the Angle Between the Two Vectors
The angle ϕ between two vectors →X and →Y can be found using the formula:
cos(ϕ)=→X⋅→Y|→X||→Y|
In our case, we have:
→X=→A×→Band→Y=→B×→A=−(→A×→B)
Thus, we can say:
→Y=−→X
Step 4: Calculate the Angle
Since →Y is the negative of →X, the angle between them is:
ϕ=π radians(or 180 degrees)
Conclusion
The angle between the vectors →A×→B and →B×→A is π radians.
---
The cross product of two vectors →A and →B is defined as:
→A×→B=|→A||→B|sin(θ)^n
where θ is the angle between the vectors →A and →B, and ^n is the unit vector perpendicular to the plane formed by →A and →B.
- The vector →A×→B is directed according to the right-hand rule and is perpendicular to the plane formed by →A and →B.
- The vector →B×→A is also directed according to the right-hand rule, but since the order of the vectors is reversed, it will point in the opposite direction. Thus, we can express it as:
→B×→A=−(→A×→B)
The angle ϕ between two vectors →X and →Y can be found using the formula:
cos(ϕ)=→X⋅→Y|→X||→Y|
In our case, we have:
→X=→A×→Band→Y=→B×→A=−(→A×→B)
Thus, we can say:
→Y=−→X
Since →Y is the negative of →X, the angle between them is:
ϕ=π radians(or 180 degrees)
The angle between the vectors →A×→B and →B×→A is π radians.
Topper's Solved these Questions
- VECTORSBook:A2ZChapter:VECTORSExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- VECTORSBook:A2ZChapter:VECTORSExercise:Assertion Reasoning
Explore 17 Videos
- VECTORSBook:A2ZChapter:VECTORSExercise:Dot Product
Explore 22 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBook:A2ZChapter:UNIT, DIMENSION AND ERROR ANALYSISExercise:Chapter Test
Explore 28 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
Knowledge Check
The cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
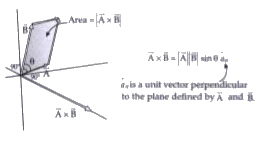
The angle between →a×→b and →b×→a is ___________.A0BπCπ2Dπ4The angle between →A+→B and →A×→B is
A0Bπ/4Cπ/2Dπ→A and →B are two Vectors and θ is the angle between them, if ∣∣→A×→B∣∣=√3(→A.→B) the value of θ is
A60∘B45∘C30∘D90∘
Find the angle between two vectors →a and →b, if ∣∣→a×→b∣∣=→a.→b.
View SolutionLet →a,→b and →c be three non-zero vectors such that no two of them are collinear and (→a×→b)×→c=13|→c|∣∣→b∣∣→a . If θ is the angle between vectors →b and →c then a value of sinθ is :
View SolutionAssertion: If θ be the angle between →A and →B, then
tanθ=→A×→B→A.→B
Reason: →A×→B is perpendicualr to →A.→B.
View SolutionThe angle between vectors →Aand→B is 60∘ What is the ratio →A.→B and ∣∣→A×→B∣∣
View SolutionIf for two vectors →A and →B,→A×→B=0, the vectors
View Solution
