ABCD is a square, EFGH is another square. AE = FB = GC = HD = a and AH = DG = CF = BE = b, then the ratio of the perimeters of ABCD to EFGH is
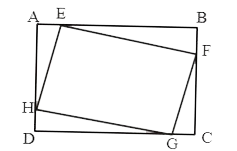
The correct Answer is:C
Step by step video, text & image solution for ABCD is a square, EFGH is another square. AE = FB = GC = HD = a and AH = DG = CF = BE = b, then the ratio of the perimeters of ABCD to EFGH is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABCD is a square and AEFG is a rectangle. Area of each of them is 36 sq. m. E is the mid-point of AB . The perimeter of the rectangle AEFG is (a) 12m (b) 18m (c) 30m (d) 36m
View SolutionIn the figure ABCD is a rectangle with AE = EF = FB, the ratio of the areas of triangle CEF and that of rectangle ABCD is

View Solution
Knowledge Check
ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A1:4B2:3C1:2D1:3ABCD is a square . Another square EFGH with the same area is placed on the square ABCD such that the point of intersection of diagonals of square ABCD and square EFGH coincide and the sides of square EFGH are parallel to the diagonals of square ABCD. Thus a new figure is formed as shown in the figure . What is the area enclosed by the given figure if each side of the square is 4 cm :
 Aa. 32(2−√2)Bb. (3+√22+√2)Cc. 32(2+√23+√2)Dd. none of these
Aa. 32(2−√2)Bb. (3+√22+√2)Cc. 32(2+√23+√2)Dd. none of theseABCD is a square with AB = (x + 16) cm and BC = ( 3 x) cm. The perimeter (in cm) of the square is
A16B24C32D96
In the figure,ABCD is a square with side x as shown. A parallelogram ABPC is drawn on the side AB as shown. Find the ratio of the area of square to the area of the parallelogram.
View SolutionIf ABCD is a square. X is a point on CD, such that DX = DO. Find ∠DOX∠XOC. O is the intersection point of diagonals.

View SolutionPQRS is a square with side 10 cm. A, B, C and D are mid-points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is
View SolutionABCD is a square of area 4, which is divided into four non overlapping triangles as shown in the fig. Then the sum of the perimeters of the triangles is

View Solution64 boys and 40 girls form a group for social work. During their membership drive, the same number of boys and girls joined the group. How many members does the group have now, if the ratio of boys to girls is 4:3 ?
View Solution
