A truck travelled from town A to town B over several days. During the first day, it covered 1/p of the total distance, where p is a natural number. During the second day, it travelled 1/q of the remaining distance, where q is a natural number. During the third day, it travelled 1/p of the distance remaining after the second day, and during the fourth day, 1/q of the distance remaining after third day. By the end of the fourth day the truck had travelled 3/4 of the distance between A and B.
The value of p + q is
A) 4
B) 5
C) 6
D) 7
The correct Answer is:D
To solve the problem step by step, we need to analyze the distances covered by the truck each day and set up equations based on the information provided.
Let the total distance between town A and town B be D.
Step 1: Distance covered on the first day
On the first day, the truck covered 1p of the total distance D.
Distance covered on Day 1=Dp
Remaining distance after Day 1:
Remaining distance=D−Dp=D(1−1p)=D(p−1p)
Step 2: Distance covered on the second day
On the second day, the truck covered 1q of the remaining distance.
Distance covered on Day 2=1q×D(p−1p)=D(p−1)pq
Remaining distance after Day 2:
Remaining distance=D(p−1p)−D(p−1)pq=D(p−1p)(1−1q)=D(p−1p)(q−1q)
Step 3: Distance covered on the third day
On the third day, the truck covered 1p of the remaining distance after Day 2.
Distance covered on Day 3=1p×D(p−1p)(q−1q)=D(p−1)(q−1)p2q
Remaining distance after Day 3:
Remaining distance=D(p−1p)(q−1q)−D(p−1)(q−1)p2q=D(p−1p)(q−1q)(1−1p)=D(p−1p)(q−1q)(p−1p)
Step 4: Distance covered on the fourth day
On the fourth day, the truck covered 1q of the remaining distance after Day 3.
Distance covered on Day 4=1q×D(p−1p)(q−1q)(p−1p)=D(p−1)2(q−1)p2q2
Remaining distance after Day 4:
Remaining distance=D(p−1p)(q−1q)(p−1p)−D(p−1)2(q−1)p2q2
Step 5: Total distance covered after four days
By the end of the fourth day, the truck had traveled 34D.
Total distance covered=Dp+D(p−1)pq+D(p−1)(q−1)p2q+D(p−1)2(q−1)p2q2=34D
Step 6: Setting up the equation
Factoring out D from the left side, we get:
1p+(p−1)pq+(p−1)(q−1)p2q+(p−1)2(q−1)p2q2=34
Step 7: Finding p+q
Through simplification and testing natural numbers for p and q, we find that p+q=7.
Final Answer
Thus, the value of p+q is:
7
On the first day, the truck covered 1p of the total distance D.
Distance covered on Day 1=Dp
Remaining distance after Day 1:
Remaining distance=D−Dp=D(1−1p)=D(p−1p)
On the second day, the truck covered 1q of the remaining distance.
Distance covered on Day 2=1q×D(p−1p)=D(p−1)pq
Remaining distance after Day 2:
Remaining distance=D(p−1p)−D(p−1)pq=D(p−1p)(1−1q)=D(p−1p)(q−1q)
On the third day, the truck covered 1p of the remaining distance after Day 2.
Distance covered on Day 3=1p×D(p−1p)(q−1q)=D(p−1)(q−1)p2q
Remaining distance after Day 3:
Remaining distance=D(p−1p)(q−1q)−D(p−1)(q−1)p2q=D(p−1p)(q−1q)(1−1p)=D(p−1p)(q−1q)(p−1p)
On the fourth day, the truck covered 1q of the remaining distance after Day 3.
Distance covered on Day 4=1q×D(p−1p)(q−1q)(p−1p)=D(p−1)2(q−1)p2q2
Remaining distance after Day 4:
Remaining distance=D(p−1p)(q−1q)(p−1p)−D(p−1)2(q−1)p2q2
By the end of the fourth day, the truck had traveled 34D.
Total distance covered=Dp+D(p−1)pq+D(p−1)(q−1)p2q+D(p−1)2(q−1)p2q2=34D
Factoring out D from the left side, we get:
1p+(p−1)pq+(p−1)(q−1)p2q+(p−1)2(q−1)p2q2=34
Through simplification and testing natural numbers for p and q, we find that p+q=7.
Thus, the value of p+q is:
7
Topper's Solved these Questions
Similar Questions
Knowledge Check
A truck travelled from town A to town B over several days. During the first day, it covered 1/p of the total distance, where p is a natural number. During the second day, it travelled 1/q of the remaining distance, where q is a natural number. During the third day, it travelled 1/p of the distance remaining after the second day, and during the fourth day, 1/q of the distance remaining after third day. By the end of the fourth day the truck had travelled 3/4 of the distance between A and B.
If the total distance is 100 kilometres, the minimum distance that can be covered on day 1 is ......... kilometres.A25B30C33D35If A travels three fifth of a certain distance on a day and the rest the next day then what part of the distance he travels on the second day?
A44260B44232C44201D44291Rahim sets out to cross a forest. On the first day, he completes 1/10th of the journey. On the second day, he covers 2/3rd of the distance travelled the first day. He continues in this manner, alternating the days in which he travels 1/10th of the distance still to be covered, with days on which he travels 2/3 of the total distance already covered. At the end of seventh day, he finds that 22½ km more will see the end of his journey. How wide is the forest?
A66 2/3kmB100kmC120kmD150km
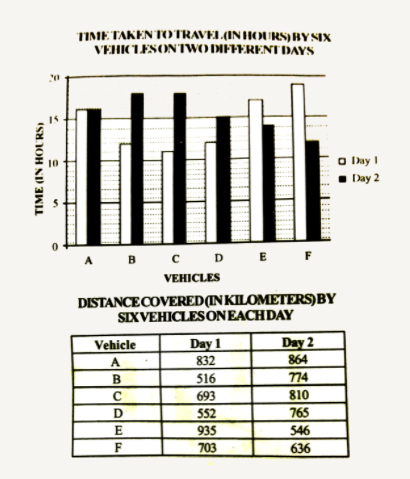
The distance travelled by vehicle F on day 2 was approximately what percent of the distance travelled by it on day 1?
View SolutionA cyclist, after cycling a distance of 70 km on the second day, find that the ratio of distance covered by him on the first two days is 4:5. If he travels a distance of 42km On the third day, then the ratio of distance travelled on the third day and the first days is
View SolutionThe Stars are not visible during the day because
View SolutionA man read 2/5 of a book on one day and 1 / 3 more than the first read on second day. If the remained pages are 15 on third day then the total pages in the book are
View SolutionDuring the days of dinosaurs , mammals had
View Solution
