In ΔABC , if DE||BC , AD =x , DB =x-2,AE=x+2andEC=x-1 , then the value of x is
The correct Answer is:x=4
To solve the problem, we will use the Basic Proportionality Theorem (BPT) which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Given Values:
- Let AD=x
- Let DB=x−2
- Let AE=x+2
- Let EC=x−1
2. Apply the Basic Proportionality Theorem:
According to BPT, since DE∥BC, we have:
ADDB=AEEC
3. Substitute the Values:
Substitute the values of AD, DB, AE, and EC into the equation:
xx−2=x+2x−1
4. Cross Multiply:
Cross multiplying gives us:
x⋅(x−1)=(x−2)⋅(x+2)
5. Expand Both Sides:
Expanding both sides:
- Left side: x2−x
- Right side: Using the difference of squares, (x−2)(x+2)=x2−4
So, we have:
x2−x=x2−4
6. Simplify the Equation:
Subtract x2 from both sides:
−x=−4
7. Solve for x:
Multiply both sides by -1:
x=4
Final Answer:
The value of x is 4.
---
- Let AD=x
- Let DB=x−2
- Let AE=x+2
- Let EC=x−1
According to BPT, since DE∥BC, we have:
ADDB=AEEC
Substitute the values of AD, DB, AE, and EC into the equation:
xx−2=x+2x−1
Cross multiplying gives us:
x⋅(x−1)=(x−2)⋅(x+2)
Expanding both sides:
- Left side: x2−x
- Right side: Using the difference of squares, (x−2)(x+2)=x2−4
So, we have:
x2−x=x2−4
Subtract x2 from both sides:
−x=−4
Multiply both sides by -1:
x=4
The value of x is 4.
Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner
15 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Long Answer Type)
7 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
Knowledge Check
In ΔABC D and E are points on sides AB and AC, such that DE || BC. If AD = x,DB = x - 2, AE = x + 2 and EC = x-1 then the value of x is
A4B2C1D8In the given figure DE || BC.

AD=x,DB=x−2
AE=x+2,EC=x−1
What is the value of x?A3B4C5D6In ΔABC, DE || BC. If AD = 2x - 1, AE = 2x + 5, BD = x - 3 and CE = x - 1, then the value of x is:
A8B9C10D11
If x+1x=2,then the value of x2+1x2 is :
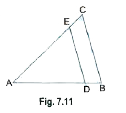
View SolutionIn Fig. 7.11, De||BC. If AD= x, DB= x- 2, AE = x + 2 and EC =x -1, find the value of x.
View SolutionIn the figure ΔABC,DE∣∣AB. If AD=2x,DC=x+3,BE=2x−1CE=x then find the value of x.

View SolutionIn ΔABC, right angled at B, if AB=12cm, BC= x and AC=13cm, then the value of x is
View SolutionIn ΔABC, when DE || BC and AD = x, DB = 3x + 4, AE = x + 3 and EC = 3x + 19 then value of x is:
View Solution

