P and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
The correct Answer is:=10 cm
To solve the problem, we will use the Basic Proportionality Theorem (also known as Thales' theorem) which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Given Ratios and Lengths:
- We are given that APPB=23.
- The length of AQ is given as 4 cm.
2. Set Up the Proportionality:
- According to the Basic Proportionality Theorem, since PQ∥BC, we have:
APPB=AQQC
- Let QC be x cm. Therefore, we can write:
23=4x
3. Cross-Multiply to Solve for x:
- Cross-multiplying gives:
2x=3×4
- Simplifying this, we find:
2x=12⟹x=122=6 cm
- Thus, QC=6 cm.
4. Calculate the Length of AC:
- Now, we can find the total length of AC:
AC=AQ+QC=4 cm+6 cm=10 cm
5. Final Answer:
- Therefore, the length of AC is 10 cm.
- We are given that APPB=23.
- The length of AQ is given as 4 cm.
- According to the Basic Proportionality Theorem, since PQ∥BC, we have:
APPB=AQQC
- Let QC be x cm. Therefore, we can write:
23=4x
- Cross-multiplying gives:
2x=3×4
- Simplifying this, we find:
2x=12⟹x=122=6 cm
- Thus, QC=6 cm.
- Now, we can find the total length of AC:
AC=AQ+QC=4 cm+6 cm=10 cm
- Therefore, the length of AC is 10 cm.
Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner
15 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Long Answer Type)
7 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
In ΔABC, D and E are points on sides AB and AC respectively such that DE∣∣BC. If AE=1.8cm, BD= 7.2cm and CE= 5.4cm, then the length of AD is
View SolutionIn ΔABC,D and E are points on the sides AB and AC respectively ,such that DE||BC. If AD=2.5cm,BD=3cm and AE =3.75 cm , then the value of AC.
View Solution
Knowledge Check
In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cmIn ΔABC,∠C=90∘ . M and N are the mid-points of sides AB and AC,respectively. CM and BN intersect each other at D and ∠BDC=90∘. If BC=8cm, then length of BN is :
A6√3 cmB6√4 cmC4√6 cmD8√3 cm
In ABC , P and Q are points on sides AB and AC respectively such that PQBC . If AP=3cm , PB=5cm and AC=8cm , find AQ .
View SolutionIf P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
View SolutionP and Q are points on sides AB and AC respectively of ΔABC . If AP = 3 cm , PB = 6 cm , AQ = 5 cm and QC = 10 , show that BC =3PQ .
View SolutionIf D and E are points on the sides AB and AC respectively of DetlaABC such that AB=5.6cm,AD=1.4cm,AC=7.2cmandAE=1.8cm. Show that DE∣∣BC.
View SolutionP and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionIn the figure, ΔABC~ΔAPQ. If AB 12 cm, and AQ =14 AC, then the length of AP is
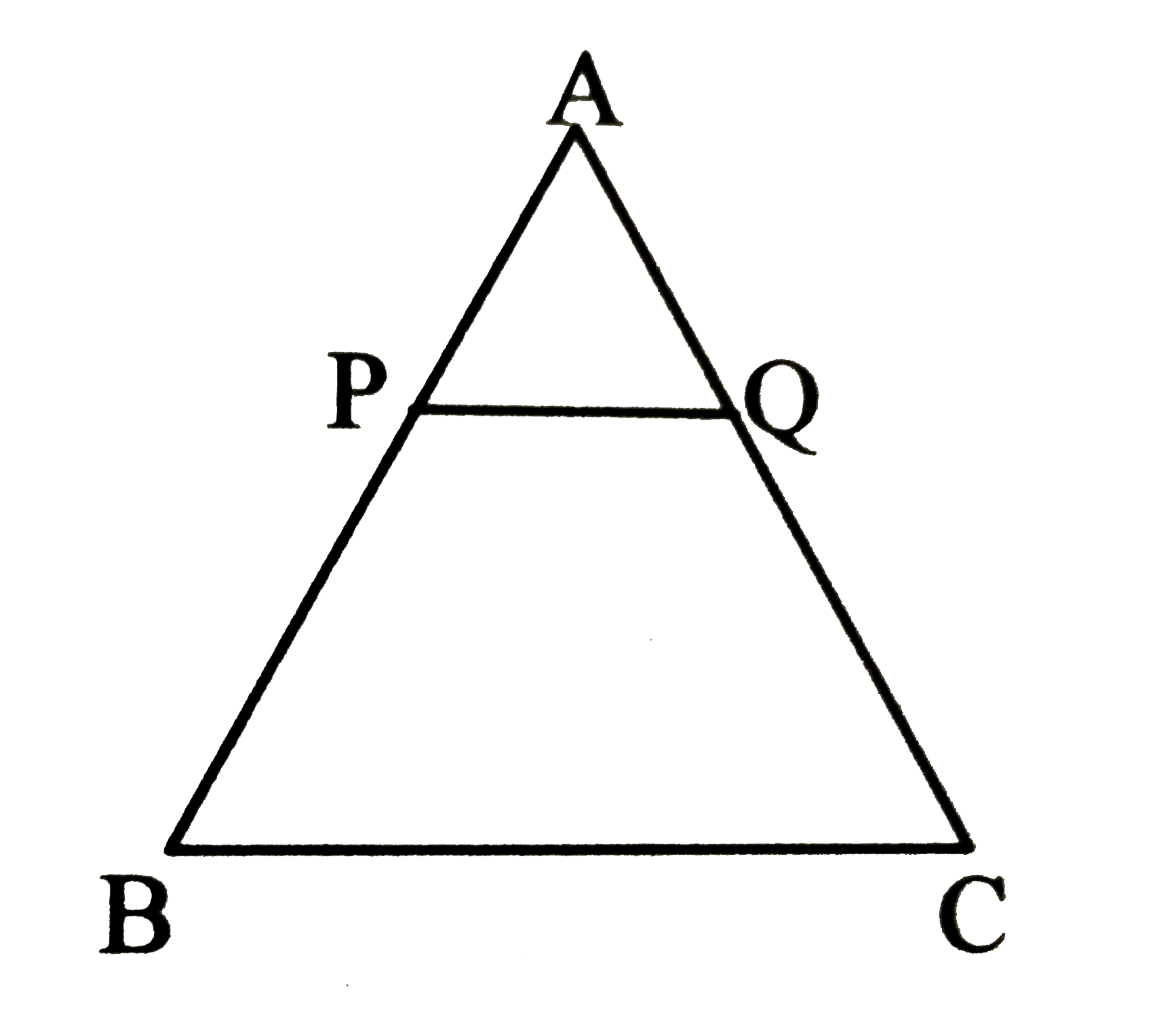
View Solution
