In the given figure, △ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that △ACD=△ABE.
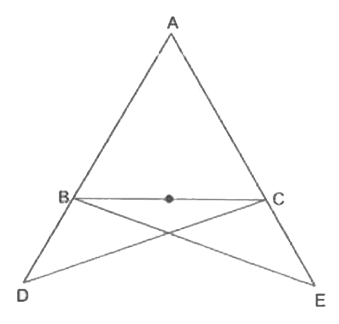
Step by step video, text & image solution for In the given figure, /_\ ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that /_\ ACD = /_\ ABE. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Match the following
2 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Assertion & Reaction Type
5 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - NCERT Section (Exercise 7.2)
20 Videos
- COMPARING QUANTITIES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner
20 Videos
- DATA HANDLINGBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner
20 Videos
Similar Questions
ABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View Solution
Knowledge Check
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
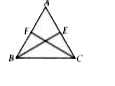 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of theseIn the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
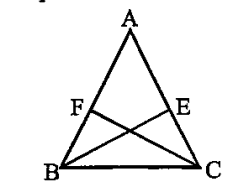 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
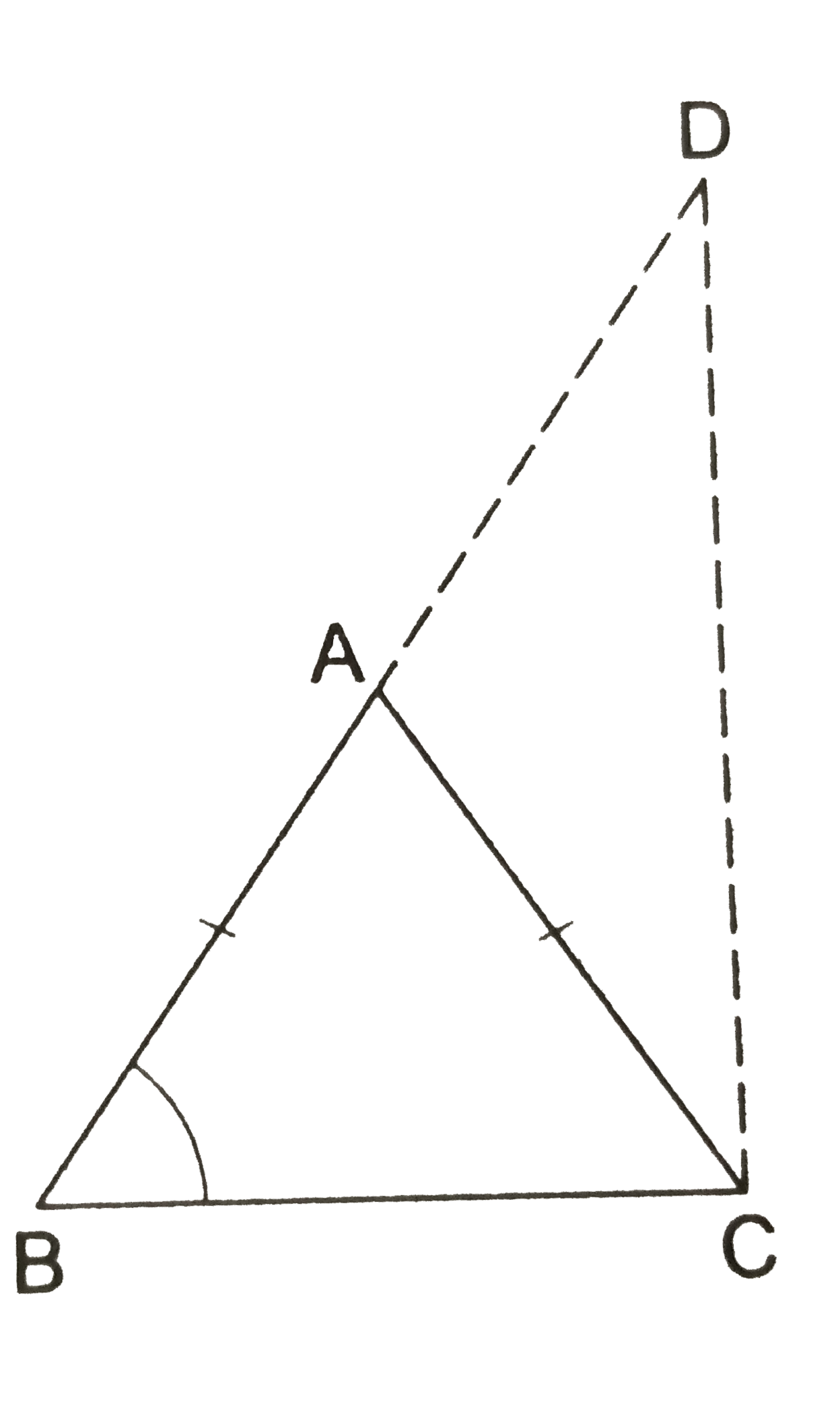
View SolutionΔABC is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that ∠BCD is a right angle.
View SolutionABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionABC is an isosceles triangle with AC = BC. If AB2−2AC2=0, prove that ABC is right triangle.
View SolutionThe incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.

View Solution
