Question

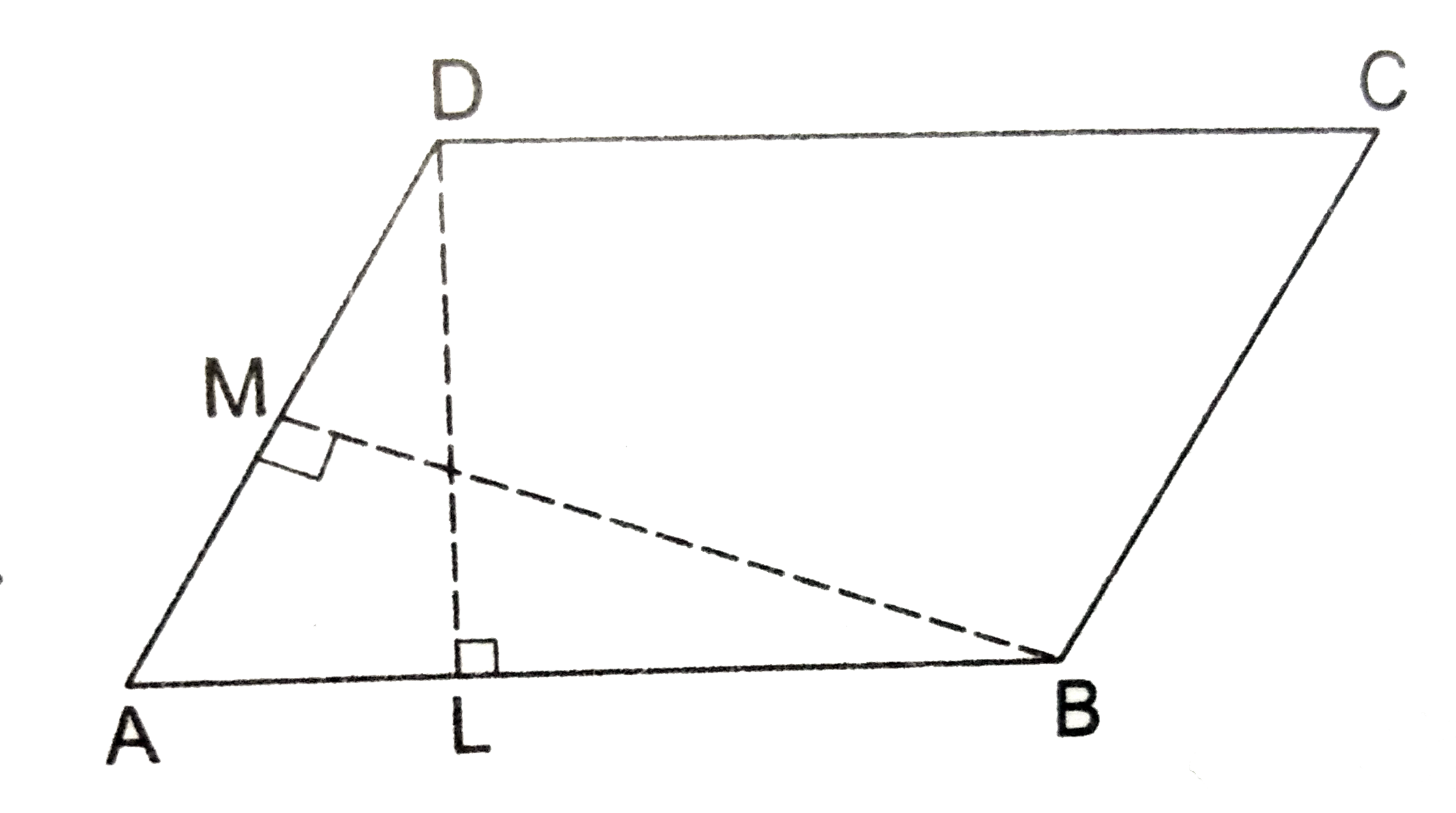
In parallelogram ABCD, let AM be the altitude corresponding to the base BC and CN the altitude corresponding to the base AB. If AB = 10 cm, AM = 6 cm and CN = 12 cm, then BC= __ cm.

Options

A. 20
B. 10
C. 12
D. 5

Answer

A

Explanation

To find the length of side BC in parallelogram ABCD, we can use the formula for the area of a parallelogram. The area can be calculated using different bases and their corresponding heights.

1. Identify the given values:
- Base AB = 10 cm
- Height CN (corresponding to base AB) = 12 cm
- Height AM (corresponding to base BC) = 6 cm

2. Calculate the area of the parallelogram using base AB:
\( \text{Area} = \text{Base} \times \text{Height} \)
Using AB as the base:
\( \text{Area} = AB \times CN = 10 \, \text{cm} \times 12 \, \text{cm} = 120 \, \text{cm}^2 \)

3. Set up the equation for the area using base BC:
Using BC as the base:
\( \text{Area} = BC \times AM \)
Therefore:
\( \text{Area} = BC \times 6 \, \text{cm} \)

4. Equate the two expressions for the area:
Since both expressions represent the area of the same parallelogram:
\( BC \times 6 = 120 \)

5. Solve for BC:
\( BC = \frac{120}{6} = 20 \, \text{cm} \)

Thus, the length of side BC is 20 cm.