In parallelogram ABCD, AB = 10 cm. The altitudes corresponding to the sides AB and AD are respectively 7 cm and 8 cm. If AD is k cm. Then value of 4 k is
The correct Answer is:35
To solve the problem, we need to find the value of 4k where k is the length of side AD in parallelogram ABCD. We are given the following information:
- AB=10cm
- The altitude corresponding to side AB (denoted as DF) is 7cm.
- The altitude corresponding to side AD (denoted as BE) is 8cm.
- AD=kcm.
1. Write the formula for the area of the parallelogram:
The area of a parallelogram can be calculated using the formula:
Area=Base×Height
2. Calculate the area using base AB:
Using AB as the base:
Area=AB×DF=10cm×7cm=70cm2
3. Calculate the area using base AD:
Using AD as the base:
Area=AD×BE=kcm×8cm=8kcm2
4. Set the two area equations equal to each other:
Since both expressions represent the area of the same parallelogram, we can set them equal:
70=8k
5. Solve for k:
To find k, divide both sides by 8:
k=708=354cm
6. Calculate 4k:
Now, we need to find 4k:
4k=4×354=35
Final Answer:
The value of 4k is 35.
---
- The altitude corresponding to side AB (denoted as DF) is 7cm.
- The altitude corresponding to side AD (denoted as BE) is 8cm.
- AD=kcm.
The area of a parallelogram can be calculated using the formula:
Area=Base×Height
Using AB as the base:
Area=AB×DF=10cm×7cm=70cm2
Using AD as the base:
Area=AD×BE=kcm×8cm=8kcm2
Since both expressions represent the area of the same parallelogram, we can set them equal:
70=8k
To find k, divide both sides by 8:
k=708=354cm
Now, we need to find 4k:
4k=4×354=35
The value of 4k is 35.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:Olympiad/HOTS Corner
Explore 14 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE ( Subjective Problems ) (Long Answer Type )
Explore 3 Videos
- CIRCLES Book:MTG IIT JEE FOUNDATIONChapter:CIRCLES Exercise:OLYMPIAD/HOTS CORNER
Explore 6 Videos
Similar Questions
Knowledge Check
In a parallelogram ABCD, AB = 12 cm and the altitude corresponding to AB is 8 cm. If AD= 10 cm, then the altitude corresponding to AD is equal to
A8.5 cmB9 cmC9.6 cmD10.8 cmIn parallelogram ABCD, let AM be the altitude corresponding to the base BC and CN the altitude corresponding to the base AB. If AB = 10 cm, AM = 6 cm and CN = 12 cm, then BC= __ cm.
A20B10C12D5Two sides of a parallelogram are 10 cm and 15 cm. If the altiude corresponding to the side of length 15 cm is 5 cm, then what is the altitude to the side of length 10 cm ?
A5 cmB7.5 cmC10 cmD15 cm
In a parallelogram ABCD, it is being given that AB = 10 cm and the altitudes corresponding to the sides AB and AD are DL = 6 cm and BM = 8 cm, respectively. Find AD.
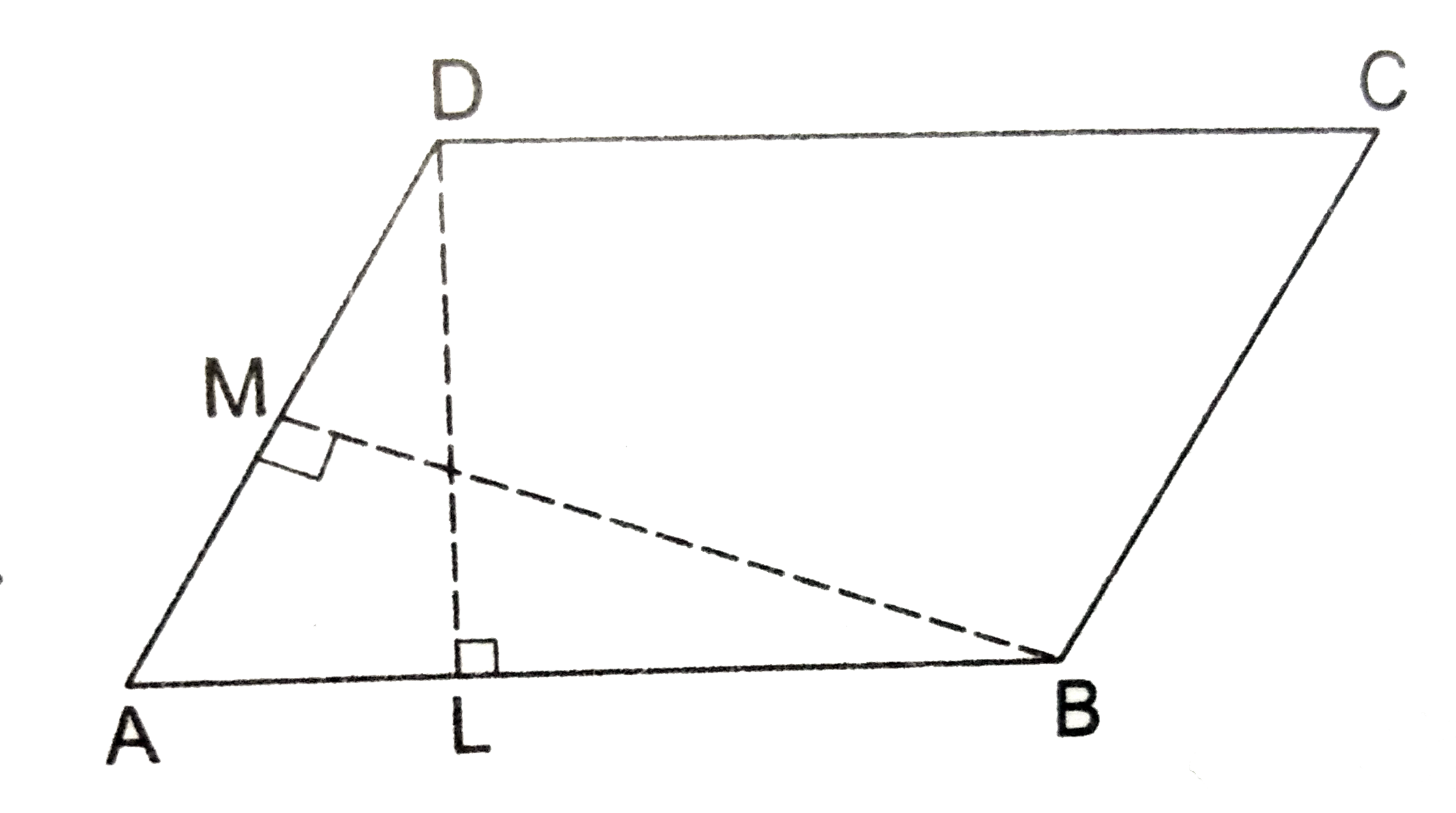
View SolutionTwo sides of a parallelogram are 10 cm and 15 cm. If the altitude corresponding to the side of length 15 cm is 5 cm, then what is the altitude to the side of length 10 cm ?
View SolutionTwo sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponding to the sides of length 25 cm is 10 cm, find the altitude corresponding to the other pair of sides.
View SolutionIn ΔABC, D and E are points on sides AB and AC respectively such that DE∣∣BC. If AE=1.8cm, BD= 7.2cm and CE= 5.4cm, then the length of AD is
View SolutionTwo sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponding to the side of length 25 cm is 10 cm, then the altitude corresponding to the other pair of sides is
View Solution