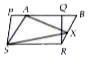
In the given figure LMNO and PMNQ are two parallelograms. R is any point on side MP. If ar(ΔNRQ) = k[ar( IIgm LMNO)] then 2k equals
![In the given figure LMNO and PMNQ are two parallelograms. R is any point on side MP. If ar(DeltaNRQ) = k[ar( I I^(gm) LMNO)] then 2k equals](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MTG_FOU_COU_MAT_IX_C09_E02_082_Q01.png)
The correct Answer is:1
Step by step video, text & image solution for In the given figure LMNO and PMNQ are two parallelograms. R is any point on side MP. If ar(DeltaNRQ) = k[ar( I I^(gm) LMNO)] then 2k equals by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Olympiad/HOTS Corner
14 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Subjective Problems ) (Long Answer Type )
3 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
Knowledge Check
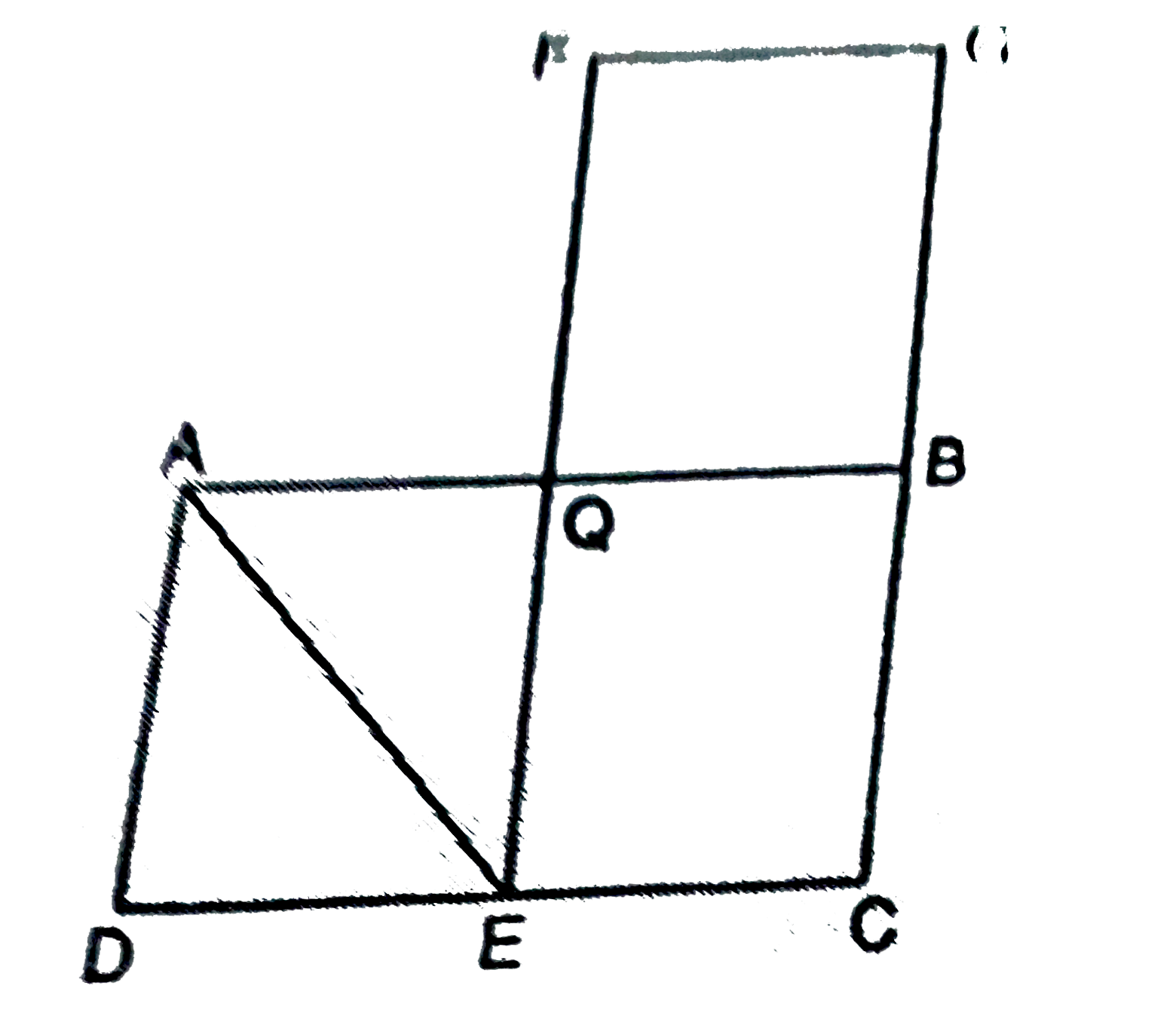
In the given figure, ABCD and AEFD a re two parallelograms.
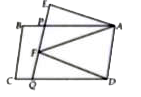
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the given figure, ABCD and AEFD a re two parallelograms.
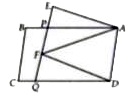
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of theseIn the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
 ATrueBFalseCPartially trueDNone of these
ATrueBFalseCPartially trueDNone of these
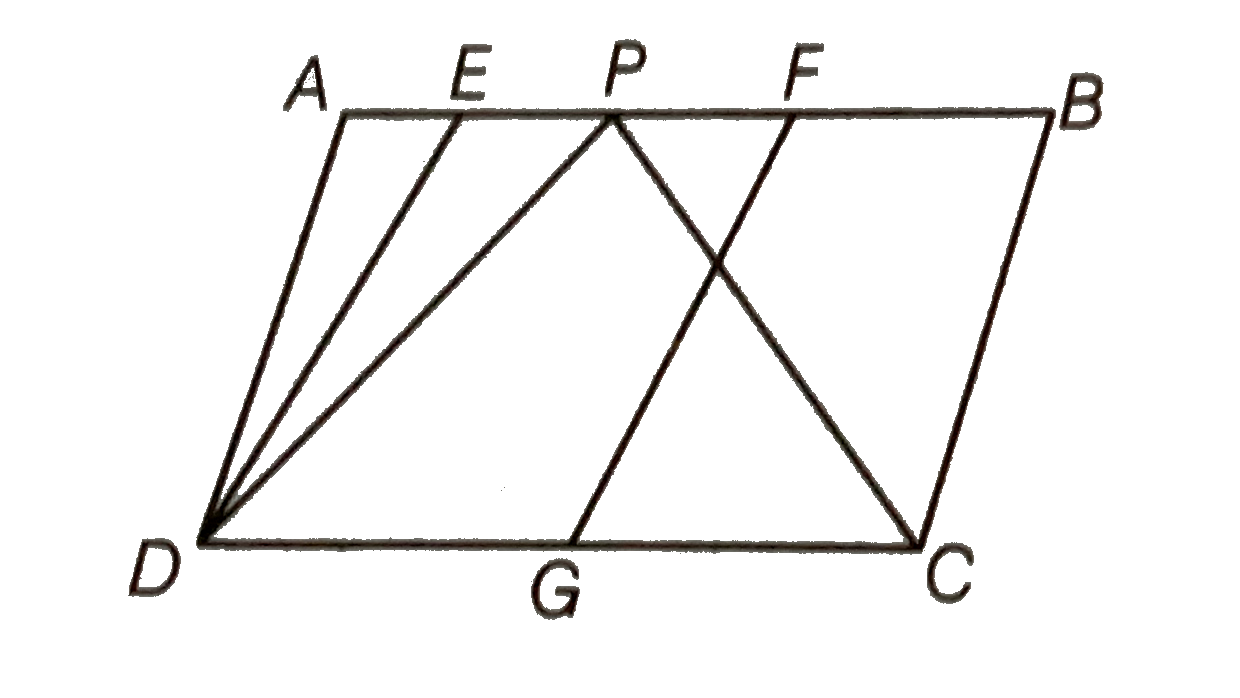
In the adjoining figure, MNPQ and ABPQ are parallelogram and T is any point on the side BP. Prove that
(i) ar(MNPQ)=ar(ABPQ)
(ii)ar(△ATQ)=12ar(MNPQ).

View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
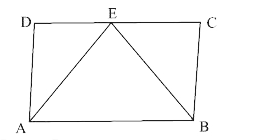
View SolutionIn given figure. If area of parallelogram ABCD is 30cm2 then find ar (ΔADE)+ ar (ΔBCE)
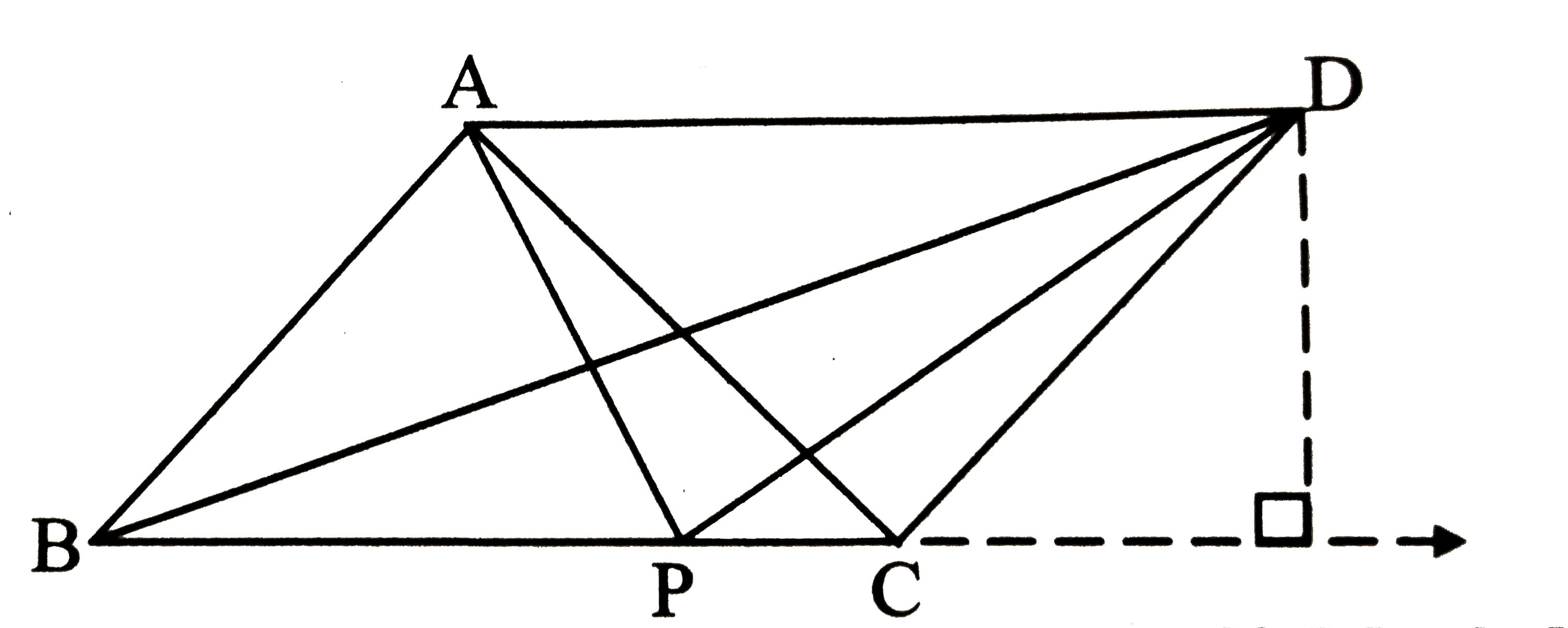
View Solution□ABCD is a parallelogram. P is any point on side BC. Find two pairs of triangles with equal areas.
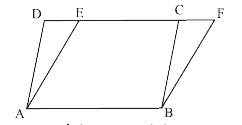
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
View Solution