In a square ABCD, AB = (4x + 3) cm and BC = (5x - 6) cm. Then, the value of x is
The correct Answer is:9
To solve the problem, we need to find the value of x given that in a square ABCD, the lengths of sides AB and BC are expressed as AB=(4x+3) cm and BC=(5x−6) cm.
1. Understand the properties of a square:
In a square, all sides are equal. Therefore, we can set the lengths of sides AB and BC equal to each other.
AB=BC
2. Set up the equation:
Substitute the expressions for AB and BC into the equation:
4x+3=5x−6
3. Rearrange the equation:
To isolate x, we will move all terms involving x to one side and constant terms to the other side. Subtract 4x from both sides:
3=5x−4x−6
Simplifying this gives:
3=x−6
4. Solve for x:
Now, add 6 to both sides to solve for x:
3+6=x
x=9
5. Conclusion:
The value of x is 9.
In a square, all sides are equal. Therefore, we can set the lengths of sides AB and BC equal to each other.
Substitute the expressions for AB and BC into the equation:
To isolate x, we will move all terms involving x to one side and constant terms to the other side. Subtract 4x from both sides:
Now, add 6 to both sides to solve for x:
The value of x is 9.
Topper's Solved these Questions
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:Olympiad/HOTS CORNER
Explore 15 Videos
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:EXERCISE (Subjective Problems) (Long Answer Type)
Explore 5 Videos
- PROBABILITYBook:MTG IIT JEE FOUNDATIONChapter:PROBABILITYExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
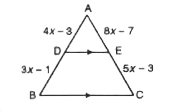
In the given figure, in ΔABC,DE∣∣BC so that AD=(4x−3)cm,AE=(8x−7)cm,BD=(3x−1)cmandCE=(5x−3)cm . Find the value of x.
View SolutionABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is:
ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?
View Solution
Knowledge Check
In a square ABCD,AB=(2x+3)cmandBC=(3x−5)cm . Then, the value of x is
A5B7C8D10In a square ABCD, AB=(2x+3) cm and BC=(3x-5) cm . Then , the value of x is
A4B5C6D8ABCD is a square with AB = (x + 16) cm and BC = ( 3 x) cm. The perimeter (in cm) of the square is
A16B24C32D96
In the given figure in ΔABC,DE∣∣BC so that , AD=(4x−3)cm,AE=(8x−7)cm,BD=(3x−1)cmandCE=(5x−3)cm. Find the value of x.
View SolutionABCD is a square with AB =(x = 16) cm and BC = (3x) cm . The perimeter (in cm ) is
View SolutionABCD is a square with AB = (x + 6) cm and BC= (3x) cm. The perimeter (in cm) is
View SolutionIf D and E are points on the sides AB and AC respectively of a triangle ABC such that DE || BC. If AD =x cm, DB =(x-3) cm, AE = ( x+ 3 ) cm and EC = ( x -2) cm, what is the value (in cm. ) of x ?
View SolutionABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is:
ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?
View Solution
