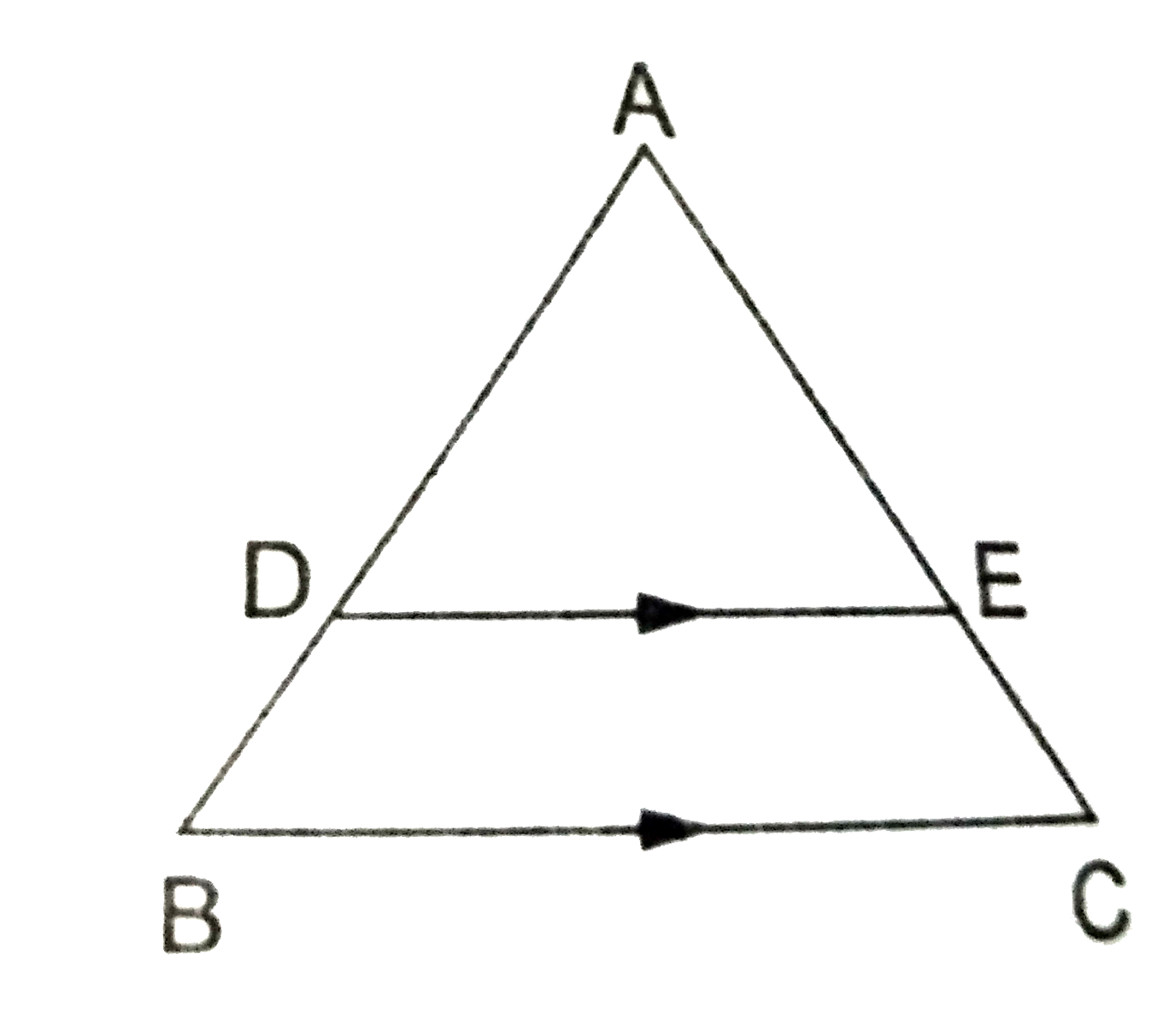
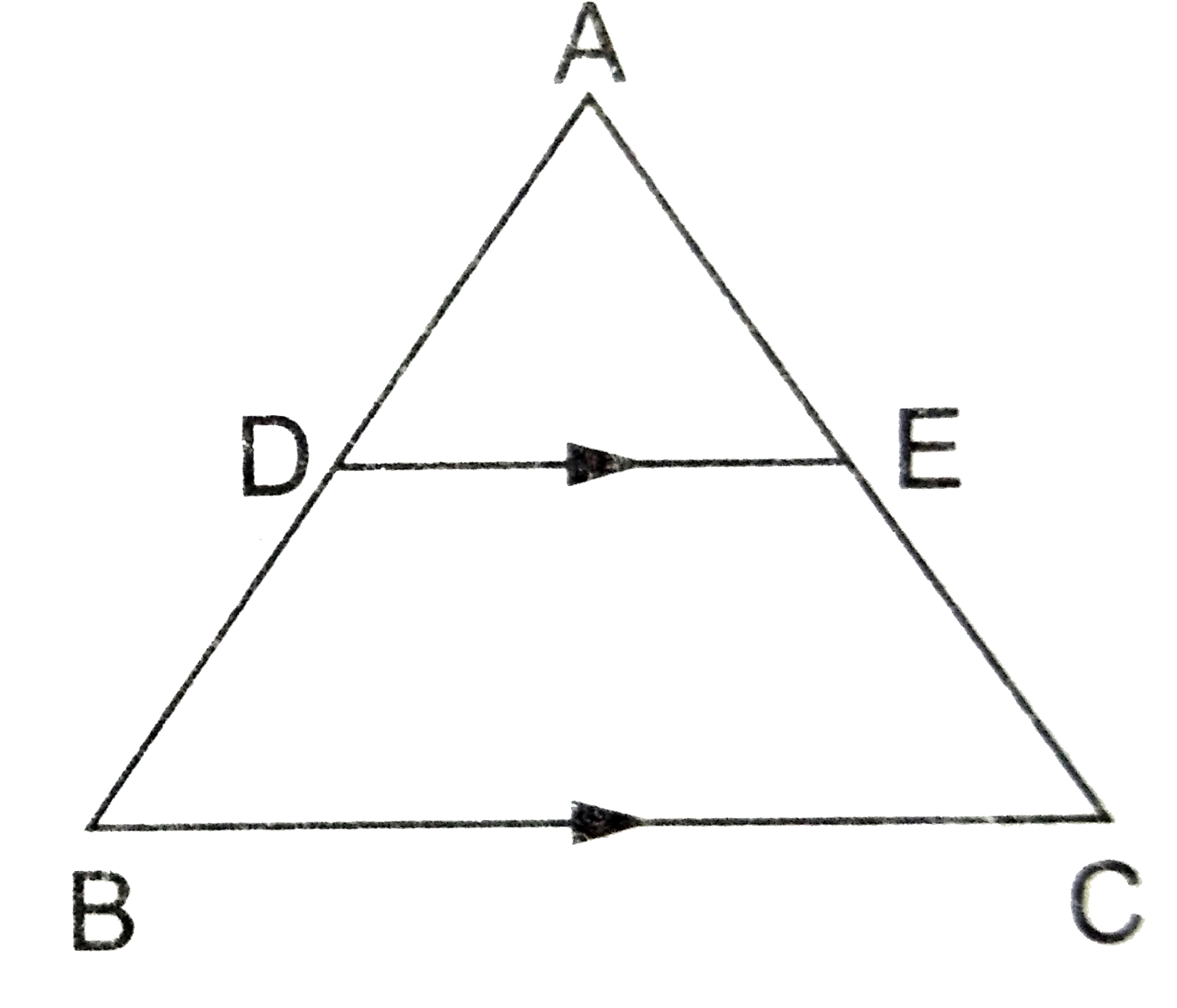
In the given figure in ΔABC,DE∣∣BC so that , AD=(4x−3)cm,AE=(8x−7)cm,BD=(3x−1)cmandCE=(5x−3)cm. Find the value of x.
A
1
B
2
C
−12
D
12
Video Solution
Text Solution
The correct Answer is:A
In ΔABC,DE∣∣BC
, ∴ADBD=AECE [ by Thale's theorem]
⇒4x−33x−1=8x−75x−3⇒(4x−3)(5x−3)=(3x−1)(8x−7)
⇒20x2−27x+9=24x2−29x+7
⇒4x2−2x−2⇒2x2−x−1=0
⇒2x2−2x+x−1=0⇒2x(x−1)+(x−1)=0
⇒(x−1)(2x+1)=0
⇒(x=1)orx=−12
But x=−12⇒AD=[4×(−12)−3]=−5.
And , distance can never be negative. So, x≠−12.
Hence x=1
|
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
In ΔABC, DE || BC. If AD = 2x - 1, AE = 2x + 5, BD = x - 3 and CE = x - 1, then the value of x is:
A8B9C10D11In a square ABCD, AB=(2x+3) cm and BC=(3x-5) cm . Then , the value of x is
A4B5C6D8
In the given figure, DE∣∣BC such that AD=xcm,DB=(3x+4)cm,AE=(x+3)cmandEC=(3x+19)cm. Find the value of x.
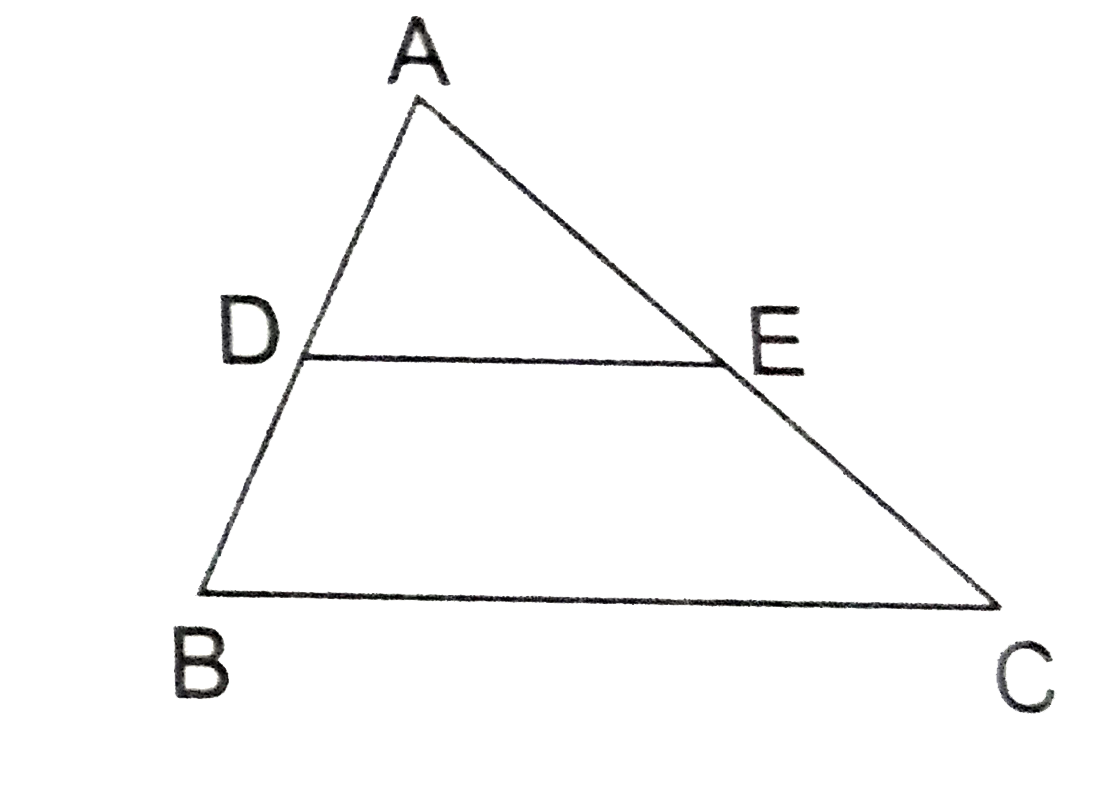
View SolutionIn the given figure, DE∣∣BC such that AD=xcm,DB=(3x+4)cmAE=(x+3)cm,andEC=(3x+19)cm. Find the value of x.
View SolutionIn ΔABC,DE∣∣BC so that AD==2.4cm,AE=3.2cmandEC=4.8cm, then , AB= ?
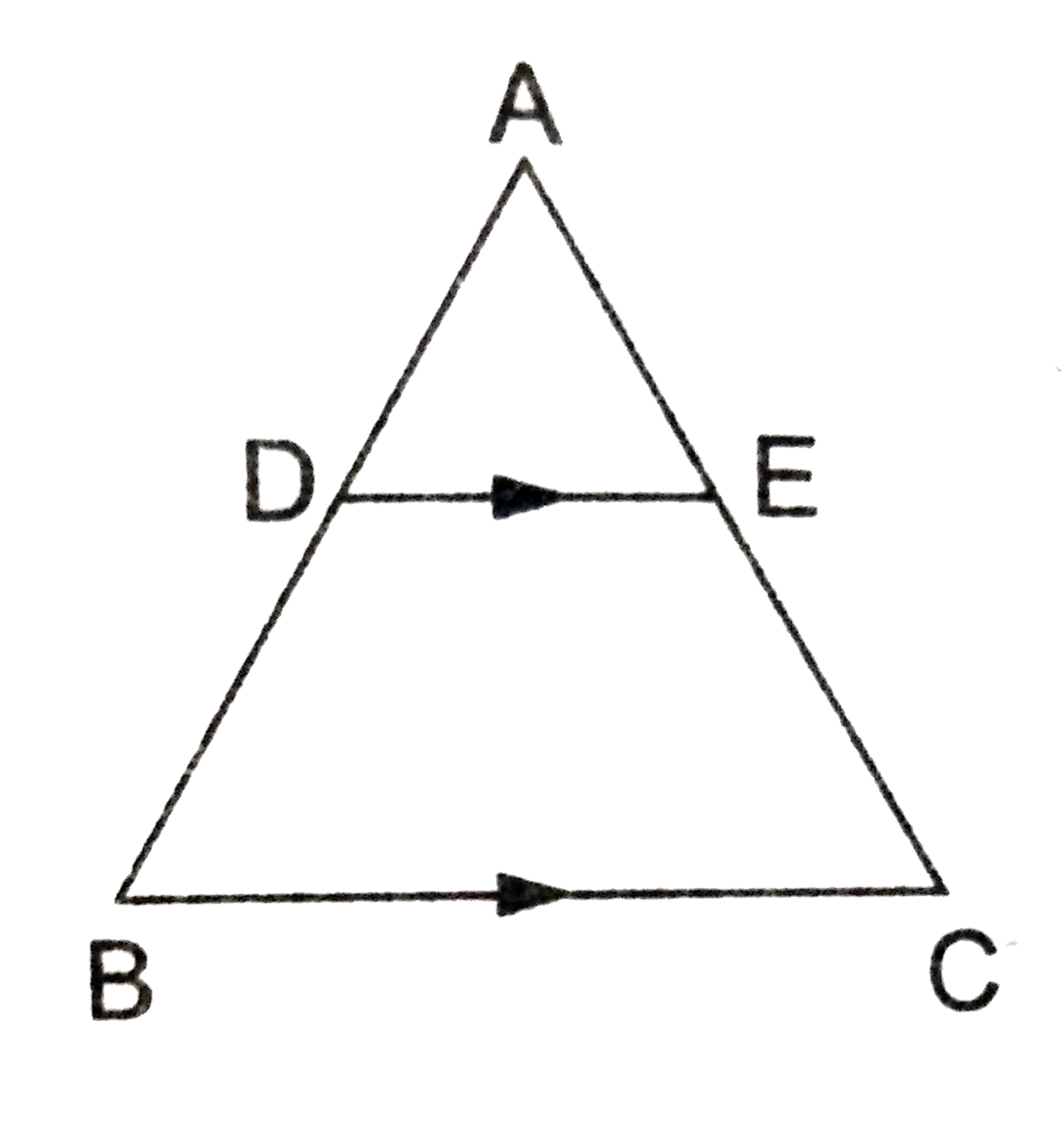
View SolutionIn ΔABC DE||BC, where DE intersects AB and AC at the points D and E, respectively. If AD = 6 cm, DB = 12X- 6cm, AE= 2x cm and CE = 16 - 2x cm, then the value of X is
View SolutionIn the figure if DE||AB, find the value of x . Given AD= (x-4).
DC= 4cm, EB= (3x-19) cm and EC= (x-3) cm.
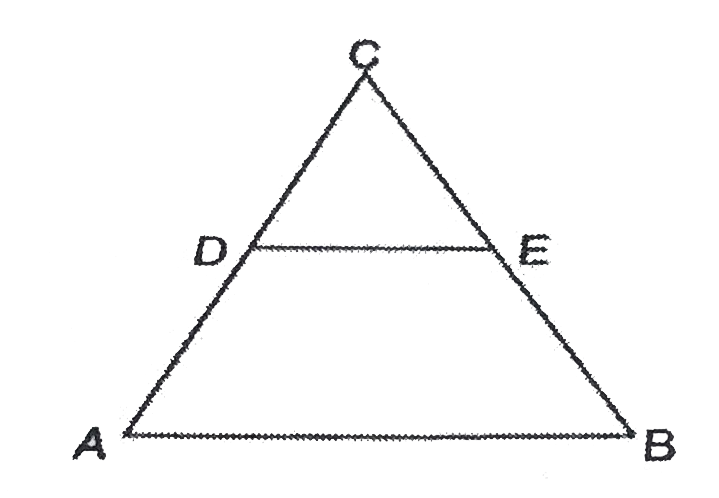
View SolutionIn ΔABC,DE∣∣BC such that ADDB=35 . If AC=5.6cm then, AE=?
View Solution