Assertion : In ΔABC,EandF are the midpoints of AC and AB respectively. The altitude AP at BC intersects FE at Q. Then, AQ = QP.
Reason : Q is the midpoint of AP.
If both assertion and reason are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If assertion is false but reason is true.
The correct Answer is:B
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Comprehension Type PASSAGE-I)3videos
QUADRILATERALS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Comprehension Type PASSAGE-II )3videos
QUADRILATERALS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Match the Following)2videos
QUADRILATERALS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER20videos
PROBABILITY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
Similar Questions
ABCD is a parallelogram. P and R are the midpoints of DC and BC respectively. The line PR intersects the diagonal AC at Q . The distance CQ will be equal to
View SolutionIn a ΔABC, D, E and F are the midpoints of BC, CA and AB respectively. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, the perimeter of ΔDEF is a cm. The value of a/2 is
View Solution
Knowledge Check
- Question 1 - Select One
In ΔABC, the line parallel to BC Intersects AB and AC at P and Q respectively. If AB:AP=5:3then AQ:QCis :
A3:2B2:3C3:5D1:2 - Question 2 - Select One
ΔABC is an equilateral triangle, AB = 6. The points P, Q and Rare midpoints of AB, BC and CA respectively. The perimeter of PBCR is
A18B15C9D12
P and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
View SolutionIn ABC , P and Q are points on sides AB and AC respectively such that PQBC . If AP=3cm , PB=5cm and AC=8cm , find AQ .
View SolutionIn ΔABC,AB=AC.A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionP and Q are points on sides AB and AC respectively of ΔABC . If AP = 3 cm , PB = 6 cm , AQ = 5 cm and QC = 10 , show that BC =3PQ .
View SolutionIn ΔABC PQ||BC. P and Q lies on side AB and AC respectively. If AB = 3AP, then what is the ratio of areas of ΔAPQandΔABC?
View SolutionIn ΔABC,D is the midpoint of BC. If DL⊥AB and DM⊥AC such that DL = DM, prove that AB = AC.
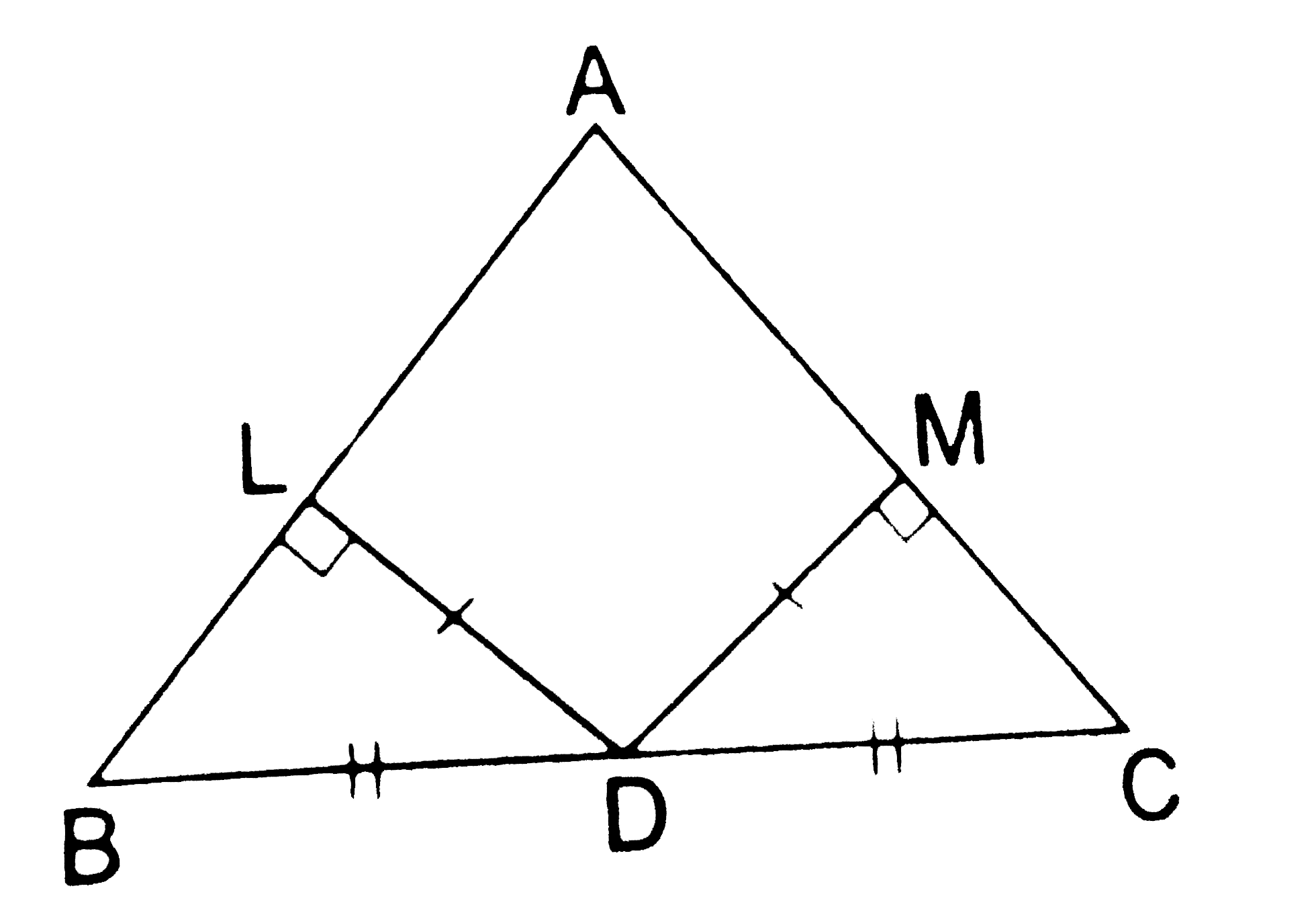 View Solution
View Solution
