The lie segments joining the midpoints of the ajdacent sides of a quadirlateral form
Parallelogram
Square
Rhombus
Rectangle
The correct Answer is:A
Step by step video, text & image solution for The lie segments joining the midpoints of the ajdacent sides of a quadirlateral form by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Match the Following)
2 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Assertion & Reason Type)
5 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )
35 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Knowledge Check
The line segments joining the midpoints of the adjacent sides of a quadrilateral form
Aa parallelogramBa rectangleCa squareDa rhombusThe figure formed by joining the midpoints of the adjacent sides of a rectangle of sides 8 cm and 6 cm is a
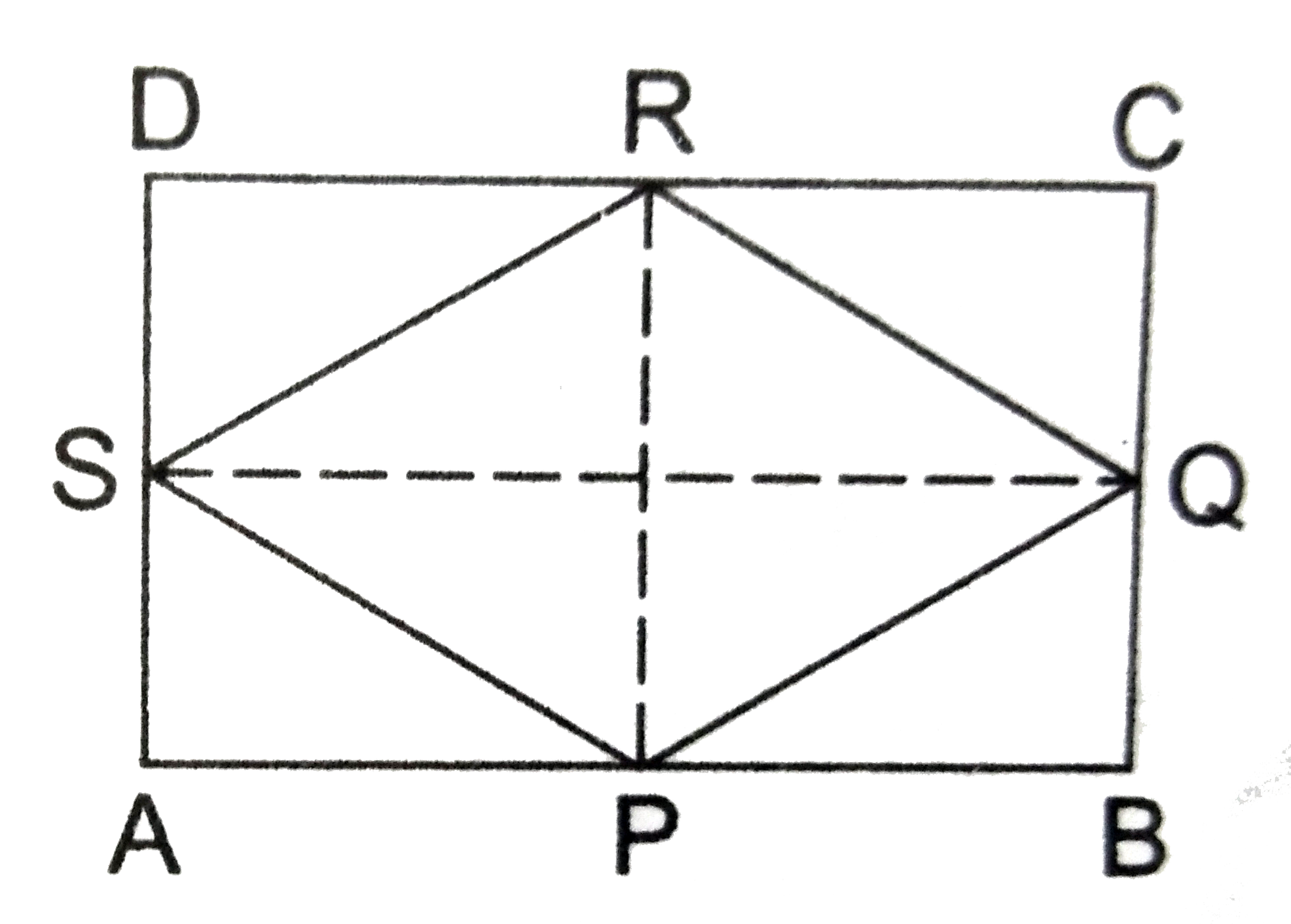 Arectangle of area 24cm2Bsquare of area 24cm2Ctrapezium of area 24cm2Drhombus of area 24cm2
Arectangle of area 24cm2Bsquare of area 24cm2Ctrapezium of area 24cm2Drhombus of area 24cm2Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC. Then DP = PC.
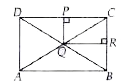
Reason : The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionProve that the line segments joining the mid-points of the sides of a triangle from four triangles, each of which is similar to the original triangle.
View SolutionThe line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
In the given figure, the side AC of ΔABC is produced to E such that CE = FAC. If D is the midpoint of BC and ED produced meets AB at F and CP, DQ are drawn parallel to BA, then FD=
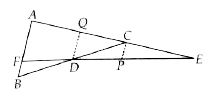
View Solution
