ABCDE... is part of a regular polygon which has interior angles of 160∘. CDLM is a square.
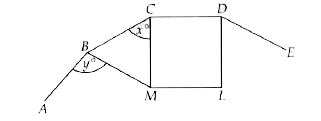
Find the value of x and y respectively.
70105
70150
105,70
150,70
The correct Answer is:A
Step by step video, text & image solution for ABCDE... is part of a regular polygon which has interior angles of 160^(@). CDLM is a square. Find the value of x and y respectively. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Match the Following)
2 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Assertion & Reason Type)
5 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )
35 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Knowledge Check
Is it possible to have a regular polygon each of whose interior angles is 100∘ ?
ANoBYesCCan not determineDNone of theseThe number of sides of a regular polygon whose interior angles are each 150∘ is :
A15B13C12D14The number of sides of a regular polygon whose interior angles are each 168∘ is:
A20B30C15D31
3.How many sides in a regular polygon has, if each of its interior angle is 135∘?
View SolutionThe number of sides of a regular polygon whose interior angles are each 168∘ is:
View SolutionHow many sides has a regular polygon each interior angle of which equals 160°.
View SolutionIn an n-sided regular polygon, each interior angle is 144∘. Find the number of the sides of the polygon.
View SolutionIn an n-sided regular polygon, each interior angle is 144∘. Find the number of the sides of the polygon.
View Solution
