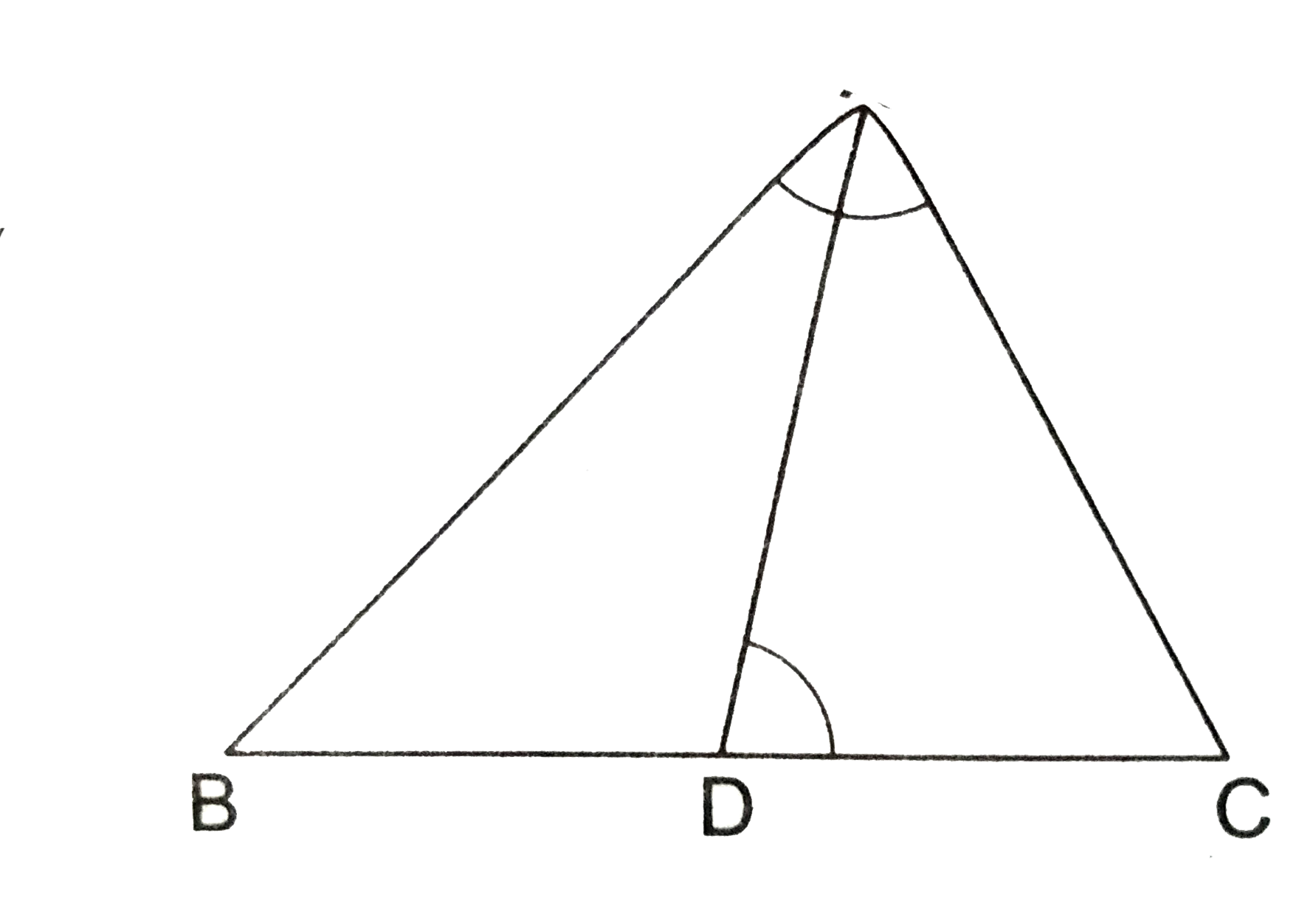
D is a point on the side BC of a such that AD bisects . Then
The correct Answer is:B
To solve the problem, we need to analyze the triangle ΔABC where D is a point on side BC such that AD bisects ∠BAC. We will use the Angle Bisector Theorem to find the relationship between the segments BD and DC.
Step 1: Understand the Angle Bisector Theorem
The Angle Bisector Theorem states that if a point D lies on the side BC of triangle ABC and AD bisects ∠BAC, then the following relationship holds:
ABAC=BDDC
This means that the ratio of the lengths of the sides opposite the angles is equal to the ratio of the segments created by the angle bisector on the opposite side.
Step 2: Set Up the Ratios
Let:
- AB=c
- AC=b
- BD=x
- DC=y
According to the Angle Bisector Theorem, we can write:
cb=xy
Step 3: Cross-Multiply
Cross-multiplying gives us:
c⋅y=b⋅x
Step 4: Analyze the Implications
From the equation c⋅y=b⋅x, we can infer that if c>b (i.e., AB>AC), then x>y (i.e., BD>DC). Conversely, if c<b, then x<y.
Step 5: Conclusion
Thus, we can conclude that the lengths of segments BD and DC are proportional to the lengths of sides AC and AB respectively. Therefore, if AB>AC, then BD>DC and vice versa.
Summary of Findings
- If AB>AC, then BD>DC.
- If AB<AC, then BD<DC.
- If AB=AC, then BD=DC.
The Angle Bisector Theorem states that if a point D lies on the side BC of triangle ABC and AD bisects ∠BAC, then the following relationship holds:
ABAC=BDDC
This means that the ratio of the lengths of the sides opposite the angles is equal to the ratio of the segments created by the angle bisector on the opposite side.
Let:
- AB=c
- AC=b
- BD=x
- DC=y
cb=xy
Cross-multiplying gives us:
c⋅y=b⋅x
From the equation c⋅y=b⋅x, we can infer that if c>b (i.e., AB>AC), then x>y (i.e., BD>DC). Conversely, if c<b, then x<y.
Thus, we can conclude that the lengths of segments BD and DC are proportional to the lengths of sides AC and AB respectively. Therefore, if AB>AC, then BD>DC and vice versa.
- If AB>AC, then BD>DC.
- If AB<AC, then BD<DC.
- If AB=AC, then BD=DC.
Topper's Solved these Questions
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:EXERCISE (Multiple Choice Questions) (LEVEL-2 )
Explore 10 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:EXERCISE (Multiple Choice Questions) (MATCH THE FOLLOWING)
Explore 2 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.5)
Explore 4 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
Knowledge Check
If D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
ABD=CDBBA>BDCBD>BADCD<CAD is a point on the side BC of △ABC such that ∠ADC=∠BAC. If CA = 12 cm and BC = 16 cm, then the length of CD is :
A12 cmB6 cmC8 cmD9 cmLet O be the in-centre of a triangle ABC and D be a point on the side BC of ΔABC, such that OD⊥BC If ∠BOD=15∘, then ∠ABC=?
A75∘B45∘C150∘D90∘
In the given figure, D and E are points on the side BC of a ΔABC such that BD = CE and AD = AE. Show that ΔABD≅ΔACE.
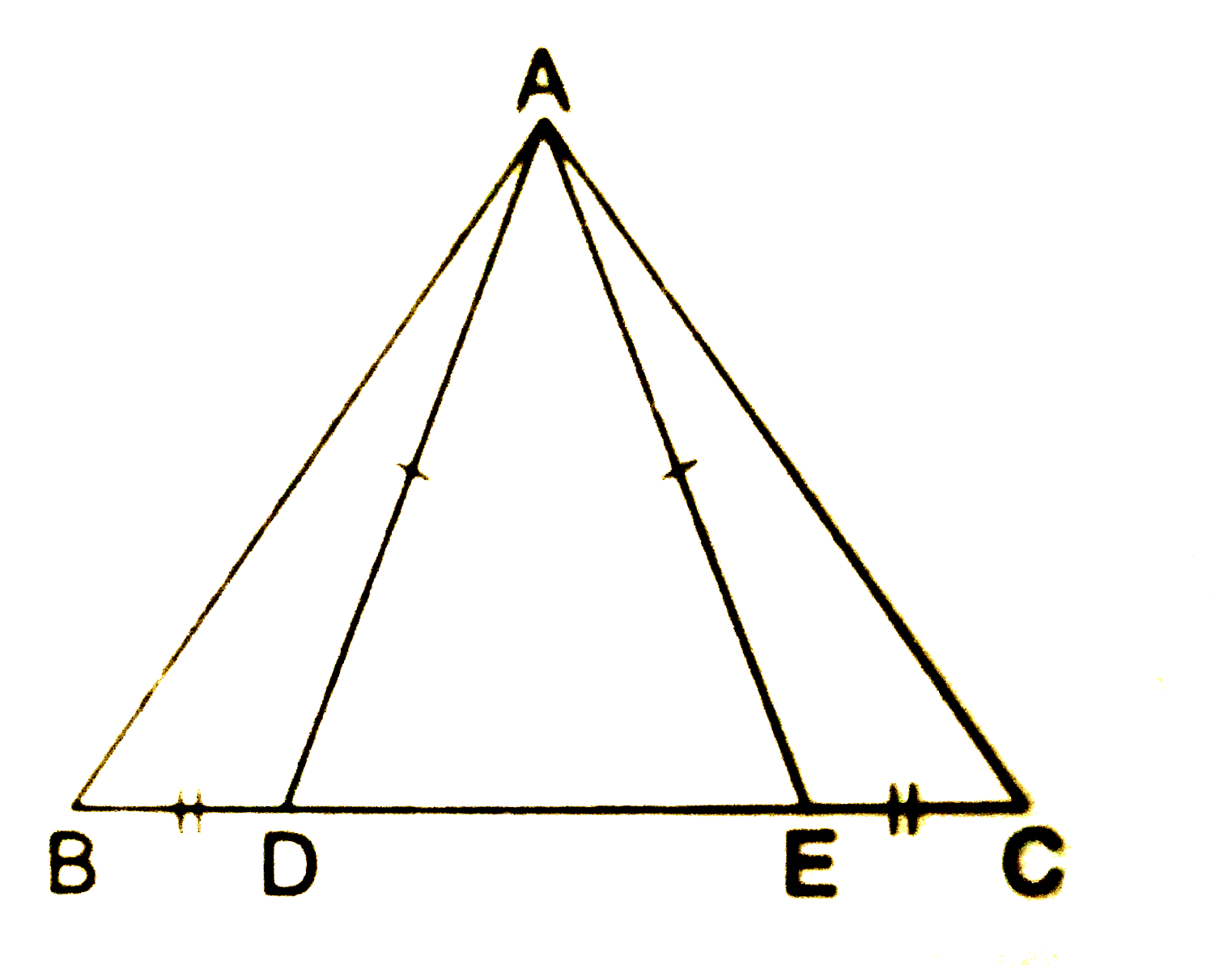
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
View SolutionIn ΔABC,∠B=2∠C. D is a point on side BC such that AD bisects ∠BACandAD=CD. Find the value of ∠BAC.
View SolutionIf D is such a point on the side, BC of ΔABC that ABAC=BDCD, then AD must be a/an:
View Solution