A metal of atomic mass 60u has a body centred cubic lattice. The edge length of the unit cell is 286 pm. Calculate the atomic radius and the density of the metal.Solution in Malayalam
From the given edge length, atomic radius for bcc crystal lattic is determined and density is calculated using the above formula.
Atomic radius for bcc lattice, pm
For bcc, pm pm
Density, (=Avogadro.s number)
Topper's Solved these Questions
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-1
50 Videos
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-2
46 Videos
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-II (ASSERTION - REASON TYPE)
20 Videos
- REDOX REACTION & ELECTROCHEMISTRYBOOK - BRILLIANT PUBLICATIONCHAPTER - REDOX REACTION & ELECTROCHEMISTRYEXERCISE - QUESTION (ELECTROCHEMISTRY) (LEVEL -II) (ASSERTION-REASON)
3 Videos
- SOLUTIONSBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLUTIONSEXERCISE - Level-III (Linked Comprehension Type)
12 Videos
Similar Questions
The radius of a di val ent cation M2+ is 94 pm and of divalent anion X2− is 146 pm. Thus, M2X2− has
View SolutionIn NaCl type structure, if all ions along an axis joining centres of the opposite face centers are missing, the expression for packing fraction in limiting case is:
View SolutionAssertion : In any ionic solid [MX] with Schottky defects, the number of positive and negative ions are same.
Reason : Equal number of cation and anion vacancies are present.
View SolutionAssertion: After the electrolysis of aqueous CuSO4 solution pH decreases.
Reason: Sulphuric acid is formed.
View Solution1 mole of A and 1 mole B are mixed together to form an ideal solution at 25∘C. Solution is placed in a vessel fitted with piston. If pressure on the solution is reduced isothermally.
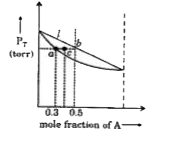
Correct relationship between P∘AandP∘B is
View SolutionIron has body centred cubic lattice. If the edge length of the unit cell is 286 pm, the radius of iron atom is
View SolutionIron crystallises in a body centred cubic structure. Calculate the radius of ioun atom if edge length of unit cell is 286 pm.
View SolutionLithium metal has a body centred cubic lattice structure with edge length of unit cell 352 pm. Calculate the density of lithium metal (Given : Atomic mass of Li = 7 g mol^(-1) )
View SolutionA metal crystallises in body centred cubic lattice with edge length of the cube 287 pm. Calculate the radius of metal atom.
View SolutionA metal crystallises with a body-centred cubic lattice. The edge length of the unit cell is 360 pm. Radius of the metal atom is
View SolutionA metal crystallizes in a body-centred cubic lattice with the unit cell length 320 pm. The radius of the metal atom (in pm) will be
View SolutionThe edge length of unit cell of a body centred metal crystal is 352 pm. Calculate the radius of an atom of the metal.
View SolutionChromium metal crystallizes in a body centred cubic lattice. The length of the unit cell edge is found to be 287 pm. Calculate the atomic radius of chromium.
View SolutionChromium metal crystallizes with a body-centred cubic lattice. The edge length of the unit cell is found to be 287 pm. Calculate the atomic radius. What would be the density of chromium in g cm−3 ? (atomic mass of Cr = 52.99)
View SolutionChromium metal crystallizes in a body centred cubic lattice. The length of the unit cell edge is found to be 287 pm. Calculate the atomic radius of chromium.
View SolutionChromium metal crystallizes with a body-centred cubic lattice. The edge length of the unit cell is found to be 287 pm. Calculate the atomic radius. What would be the density of chromium in g cm−3 ? (atomic mass of Cr = 52.99)
View Solution
