An alloy of silver and copper crystallizes in a cubic lattice in which silver atoms occupy the lattice points at the comers of a cube and copper atoms occupy the face centres of the cube. Determine the formula of the compoundSolution in Malayalam
One-eighth of each silver atom and one-half of each copper are contained within the unit cell of the compound.
Number of Ag atoms per unit cell=8(1/8)=1
Number of Cu atoms per unit cell=6(1/2)=3
The formula of the compound is AgCu3.
Topper's Solved these Questions
- SOLID STATEBook:BRILLIANT PUBLICATIONChapter:SOLID STATEExercise:LEVEL-1
Explore 50 Videos
- SOLID STATEBook:BRILLIANT PUBLICATIONChapter:SOLID STATEExercise:LEVEL-2
Explore 46 Videos
- SOLID STATEBook:BRILLIANT PUBLICATIONChapter:SOLID STATEExercise:LEVEL-II (ASSERTION - REASON TYPE)
Explore 20 Videos
- REDOX REACTION & ELECTROCHEMISTRYBook:BRILLIANT PUBLICATIONChapter:REDOX REACTION & ELECTROCHEMISTRYExercise:QUESTION (ELECTROCHEMISTRY) (LEVEL -II) (ASSERTION-REASON)
Explore 3 Videos
- SOLUTIONSBook:BRILLIANT PUBLICATIONChapter:SOLUTIONSExercise:Level-III (Linked Comprehension Type)
Explore 12 Videos
Similar Questions
The radius of a di val ent cation M2+ is 94 pm and of divalent anion X2− is 146 pm. Thus, M2X2− has
View SolutionIn NaCl type structure, if all ions along an axis joining centres of the opposite face centers are missing, the expression for packing fraction in limiting case is:
View SolutionAssertion : In any ionic solid [MX] with Schottky defects, the number of positive and negative ions are same.
Reason : Equal number of cation and anion vacancies are present.
View SolutionAssertion: After the electrolysis of aqueous CuSO4 solution pH decreases.
Reason: Sulphuric acid is formed.
View Solution1 mole of A and 1 mole B are mixed together to form an ideal solution at 25∘C. Solution is placed in a vessel fitted with piston. If pressure on the solution is reduced isothermally.
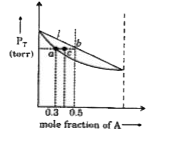
Correct relationship between P∘AandP∘B is
View SolutionAn alloy of copper and gold crystallizes in cubic lattic, in which the Au− atoms occupy the lattice points at the corners of cube and Cu− atoms occupy the centre of each face. The formula of this alloy is :
View SolutionA compound of A and B crystallizes in a cubic lattice in which A atoms occupy the lattice points at the corners of a cube and two atoms of B occupy the center of each of the cube faces. What is the formula of this compound?
View SolutionAn alloy of copper, silver and gold is found to have copper forming the simple cubic close packed lattice. If the silver atoms occupy the face centres and gold is present at the body centre, then the formula of the alloy will be
View SolutionA compound alloy of gold and copper crystallizes in a cubic lattice in which gold occupy that lattice point at corners of the cube and copper atom occupy the centres of each of the cube faces. What is the formula of this compound.
View SolutionA compound alloy of gold and copper crystallizes in a cubic lattice in which gold occupy that lattice point at corners of the cube and copper atom occupy the centres of each of the cube faces. What is the formula of this compound.
View SolutionA compound alloy of gold copper crystallies in a cubic lattice in which gold atoms occupy the lattice points at the corners of each cube and copper atoms occupy the centres of each cubic faces. Find the number of total atoms per unit cell.
View SolutionA compound representing alloy of gold and copper crystallises in a cubic lattice in which gold atoms occupy the lattice points at the corners of a cube and copper atoms occupy the centres of each of the cubic faces. Find formula of compound.
View SolutionA compound AxBy crystallises on a fcc lattice in which A occupies each corner of a cube and B occupies the centre of each face of the cube. What is the formula of the compound ?
View SolutionAn alloy of copper and gold crystallizes in cubic lattic, in which the Au− atoms occupy the lattice points at the corners of cube and Cu− atoms occupy the centre of each face. The formula of this alloy is :
View SolutionA compound alloy of gold and Cu crystallises in a cubic lattice in which the gold atoms occupy the lattice points at the comers of a cube and the copper atoms occupy the centres of each of the cube faces. What is the empirical formula of this compound ?
View SolutionA compound alloy of gold and Cu crystallises in a cubic lattice in which the gold atoms occupy the lattice points at the comers of a cube and the copper atoms occupy the centres of each of the cube faces. What is the empirical formula of this compound ?
View Solution

