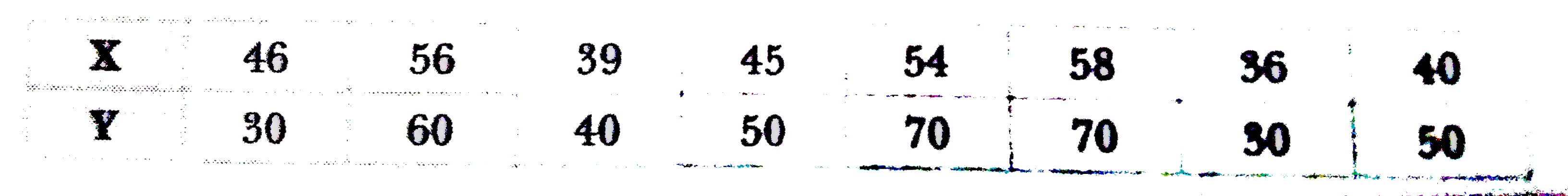If the two lines of regression are 3x+2y=26and6x+y=31, then the coefficient of correlation between x and y is ……………..
The correct Answer is:−12
To find the coefficient of correlation between x and y given the two lines of regression 3x+2y=26 and 6x+y=31, we will follow these steps:
Step 1: Convert the regression equations into slope-intercept form
1. First Equation: 3x+2y=26
- Rearranging gives:
2y=−3x+26
- Dividing by 2:
y=−32x+13
- Here, the slope bxy=−32.
2. Second Equation: 6x+y=31
- Rearranging gives:
y=−6x+31
- Here, the slope byx=−6.
Step 2: Find the product of the slopes
Now, we need to find the product of the slopes bxy and byx:
bxy=−32,byx=−6
Calculating the product:
bxy⋅byx=(−32)⋅(−6)=3⋅62=182=9
Step 3: Calculate the coefficient of correlation
The coefficient of correlation r is given by:
r=√bxy⋅byx
Substituting the product we found:
r=√9=3
Conclusion
Thus, the coefficient of correlation between x and y is:
3
1. First Equation: 3x+2y=26
- Rearranging gives:
2y=−3x+26
- Dividing by 2:
y=−32x+13
- Here, the slope bxy=−32.
- Rearranging gives:
y=−6x+31
- Here, the slope byx=−6.
Now, we need to find the product of the slopes bxy and byx:
bxy=−32,byx=−6
Calculating the product:
bxy⋅byx=(−32)⋅(−6)=3⋅62=182=9
The coefficient of correlation r is given by:
r=√bxy⋅byx
Substituting the product we found:
r=√9=3
Thus, the coefficient of correlation between x and y is:
3
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - PROBLEM SET (1) (TRUE AND FALSE)9videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - SELF ASSESSMENT TEST10videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - PROBLEM SET (1) TRUE/FALSE6videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test13videos
CONCEPTS OF SET THEORY
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)1videos
DEFINITE INTEGRAL
Similar Questions
Knowledge Check
- Question 1 - Select One
If the two lines of regression are 3x+y=15andx+4y=3, then value of x when y=3 is
A−4B−8C4Dnone of these - Question 2 - Select One
If the lines of regression are 3x+12y=19 and 3y+9x=46 then r will be
A0.289B−0.289C0.209D0.409 - Question 3 - Select One
If two lines of regression are perpendicular, then the correlation coefficient r is
A2B12C0DNone of these
Angle between lines of regression of the variables x and y with coefficient of correlation r is …………….
View SolutionFind the Kari Pearson's Coefficient of correlation between x and y for the data
 View Solution
View SolutionIf two lines of regression are perpendicular, then the correlation coefficient r is
View SolutionLet 5x+3y=55 and 7x+y=45 be two lines of regression for a bivariate data
Coefficient of correlation between x and yView SolutionThe coefficient of correlation between X and Y is 0.6 U and V are two variables defined as U=x−32,V=y−23, then the coefficient of correlation between U and V is
View Solution