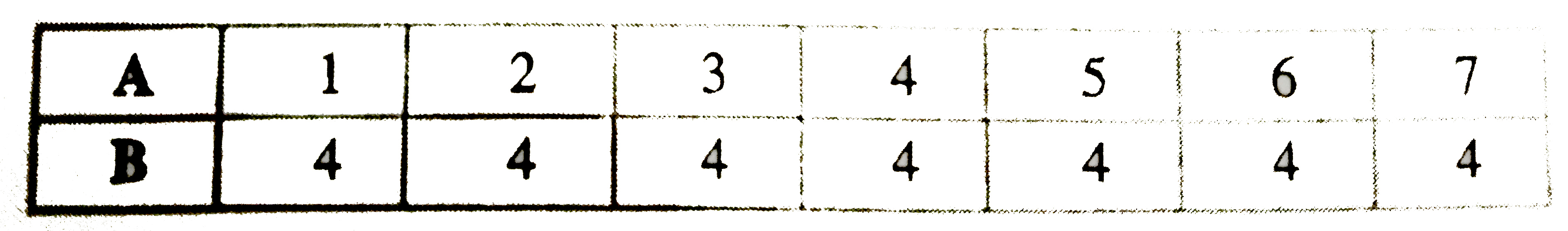If coefficient of correlation , then r is called ……………..
The correct Answer is:perfect and negative
To solve the question, we need to understand the meaning of the correlation coefficient r.
1. Understanding Correlation Coefficient: The correlation coefficient r is a statistical measure that describes the strength and direction of a relationship between two variables. The value of r can range from -1 to 1.
2. Identifying the Value of r: In this case, we are given that r=−1.
3. Interpreting r=−1: When r is equal to -1, it indicates a perfect negative correlation between the two variables. This means that as one variable increases, the other variable decreases in a perfectly linear manner.
4. Conclusion: Therefore, if the correlation coefficient r is -1, we call it "perfectly negatively correlated".
Final Answer:
If the coefficient of correlation r=−1, then r is called perfectly negatively correlated.
---
If the coefficient of correlation r=−1, then r is called perfectly negatively correlated.
Topper's Solved these Questions
- CORRELATION AND REGRESSION Book:ML KHANNAChapter:CORRELATION AND REGRESSION Exercise:PROBLEM SET (1) (TRUE AND FALSE)
Explore 9 Videos
- CORRELATION AND REGRESSION Book:ML KHANNAChapter:CORRELATION AND REGRESSION Exercise:SELF ASSESSMENT TEST
Explore 10 Videos
- CORRELATION AND REGRESSION Book:ML KHANNAChapter:CORRELATION AND REGRESSION Exercise:PROBLEM SET (1) TRUE/FALSE
Explore 6 Videos
- CONCEPTS OF SET THEORY Book:ML KHANNAChapter:CONCEPTS OF SET THEORY Exercise:Self Assessment Test
Explore 13 Videos
- DEFINITE INTEGRALBook:ML KHANNAChapter:DEFINITE INTEGRALExercise:Miscellaneous Questions (Assertion/Reason)
Explore 1 Video
Similar Questions
Knowledge Check
Coefficient of correlation is the measure of
Acentral tendencyBdispresionCboth central tendency and dispersionDneither central tendency nor dispersionBOD is measure of
ACentral tendencyBDispersionCBoth central tendency and dispersionDNeither central tendency nor dispersion.The coefficient of correlation is independent of
Achange of scale onlyBchange of origin onlyCboth change of scale and change of originDneither change of scale nor change or origin
Angle between lines of regression of the variables x and y with coefficient of correlation r is …………….
View SolutionCalculate the coefficient of correlation between the two series :

View SolutionCalculated coefficient of correlation between the price and quantity demanded.
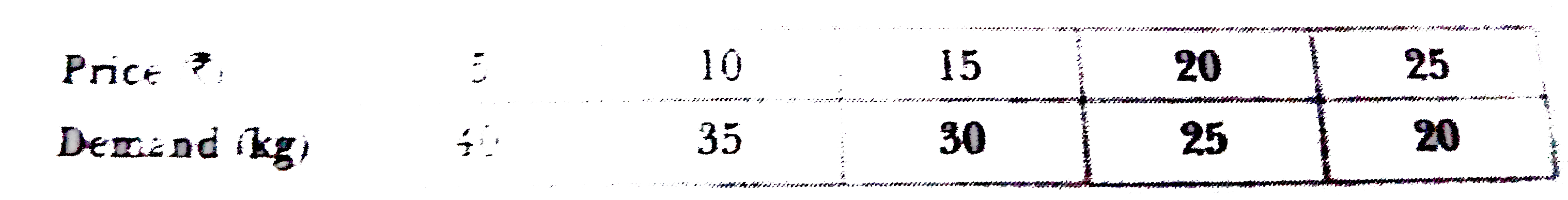
View SolutionCalculate coefficient of correlation between the price and quantity supplied.
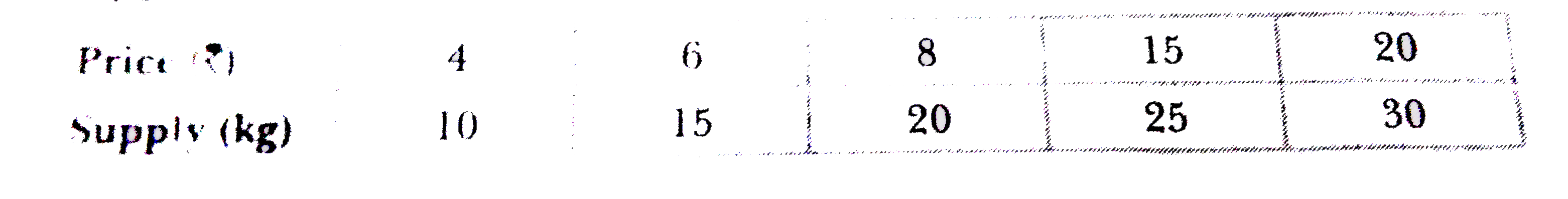
View SolutionIf r is the coefficient of correlation between two variable, then
View Solution