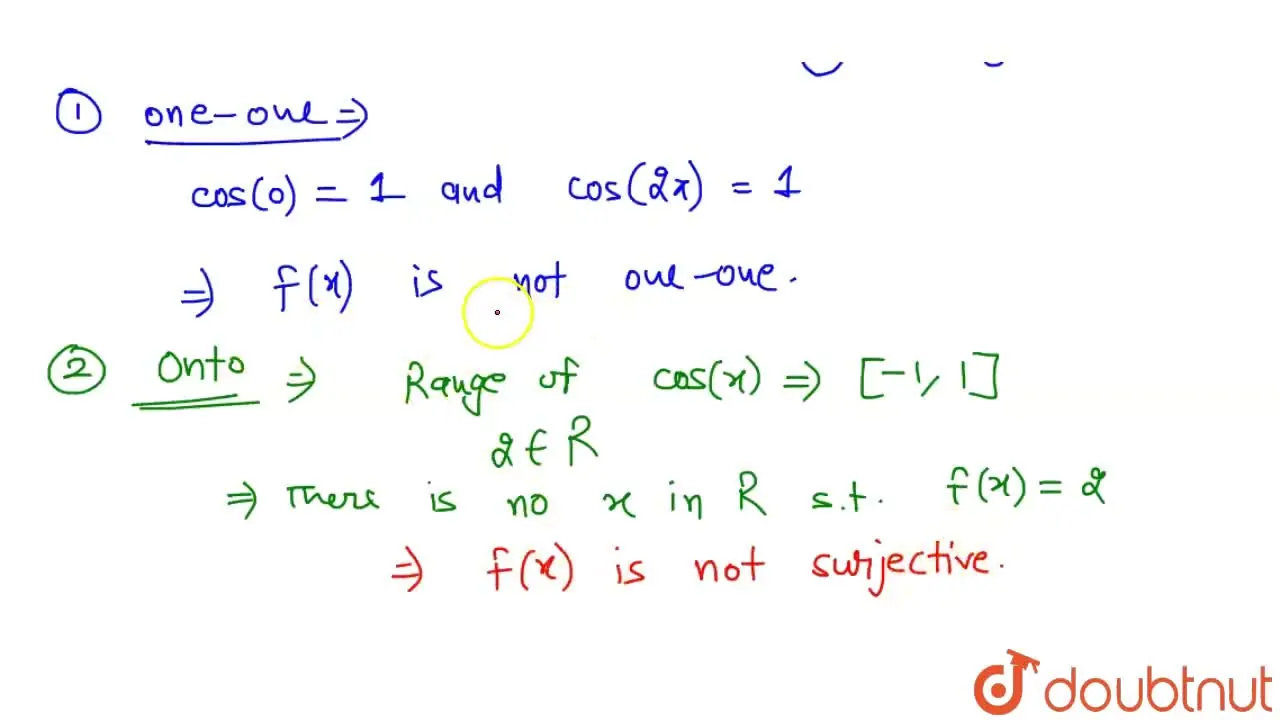A mapping is defined as f:R→R. f (x) = cos x. Show that it is neither one-one nor surjective.
Step by step video, text & image solution for A mapping is defined as f:R to R. f (x) = cos x. Show that it is neither one-one nor surjective. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ML KHANNACHAPTER - FUNCTIONSEXERCISE - PROBLEM SET (3)71videos
FUNCTIONS
- BOOK - ML KHANNACHAPTER - FUNCTIONSEXERCISE - PROBLEM SET (4)43videos
FUNCTIONS
- BOOK - ML KHANNACHAPTER - FUNCTIONSEXERCISE - SELF ASSESSMENT TEST10videos
FUNCTIONS
- BOOK - ML KHANNACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIES EXERCISE - Problem Set (2) (Self Assessment Test)8videos
EXPONENTIAL AND LOGARITHMIC SERIES
- BOOK - ML KHANNACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Problem Set (3) FILL IN THE BLANKS9videos
HEIGHTS AND DISTANCES
Similar Questions
A mapping is defined as f:R→R. f (x) = cos x. Show that it is neither one-one nor surjective.
View SolutionLet the function f:R→R be defined by f(x)=cosx,∀x∈R. Show that f is neither one-one nor onto.
View SolutionIf x={1,−1} and mapping is defined as f:X→X,f(x)=x2, then prove that this mapping is not one-one onto.
View SolutionA mapping f: R → R which is defined as f(x) = cos x: x ∈ R is:
View SolutionA mapping f: R → R which is defined as f(x) = cos x: x ∈ R is:
View SolutionLet f:R→R defined by f(x)=x21+x2. Proved that f is neither injective nor surjective.
View SolutionMapping f:R→R which is defined as f(x)=cosx,x∈R will be
View SolutionShow that the function f:R→R given by f(x)=cosxforallx∈R, is neither one-one nor onto
View SolutionShow that the function f:R→R:f(x)=sinx is neither one-one nor onto
View SolutionShow that the fucntion f:R→R:f(x)=x4 is neither one-one not noto.
View Solution