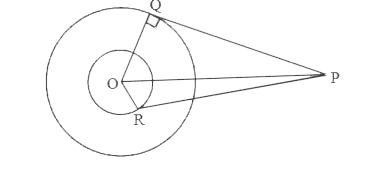
The circle of radius 4 cm and centre O has a tangent PR. If ∠POR=90∘ and OR = 7 cm and OP=24cm. Calculate the length (in cm.) of PR.
20
24
25
35
The correct Answer is:C
To solve the problem, we will use the Pythagorean theorem, which applies to right-angled triangles. Here are the steps:
Step 1: Understand the Geometry
We have a circle with center O and radius 4 cm. The tangent line PR touches the circle at point R. We know that angle POR is 90 degrees, OR is 7 cm, and OP is 24 cm.
Step 2: Identify the Triangle
In triangle POR, we have:
- OP (the distance from point O to point P) = 24 cm (hypotenuse)
- OR (the distance from point O to point R) = 7 cm (one leg)
- PR (the length of the tangent) = ? (the other leg)
Step 3: Apply the Pythagorean Theorem
According to the Pythagorean theorem:
PR2+OR2=OP2
Step 4: Substitute the Known Values
Substituting the values we have:
PR2+72=242
Calculating the squares:
PR2+49=576
Step 5: Solve for PR^2
Now, isolate PR^2:
PR2=576−49
PR2=527
Step 6: Calculate PR
Now, take the square root of both sides to find PR:
PR=√527
Step 7: Simplify the Square Root
Calculating the square root:
PR≈22.9 cm
Final Answer
The length of PR is approximately 22.9 cm.
---
We have a circle with center O and radius 4 cm. The tangent line PR touches the circle at point R. We know that angle POR is 90 degrees, OR is 7 cm, and OP is 24 cm.
In triangle POR, we have:
- OP (the distance from point O to point P) = 24 cm (hypotenuse)
- OR (the distance from point O to point R) = 7 cm (one leg)
- PR (the length of the tangent) = ? (the other leg)
According to the Pythagorean theorem:
PR2+OR2=OP2
Substituting the values we have:
PR2+72=242
PR2+49=576
Now, isolate PR^2:
PR2=576−49
PR2=527
Now, take the square root of both sides to find PR:
PR=√527
Calculating the square root:
PR≈22.9 cm
The length of PR is approximately 22.9 cm.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
Explore 90 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
Explore 90 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
PR is tangent to a circle, with centre O and radius 4 cm, at point Q. If ∠POR=90∘,OR=5cmand OP=203cm, then (in cm) the length of PR :
A3B163C233D253In Fig. 1, on a circle of radius 7 cm, tangent PT is drawn from a point P such that PT = 24 cm. If O is the centre of the circle, then the length of PR is
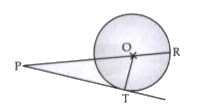 A30 cmB28 cmC32 cmD25 cm
A30 cmB28 cmC32 cmD25 cmPR is a tangent at a point Q on a circle, in which Q is the centre and its radius is 8 cm. If OR = 16 cm and OP = 10 cm, then the length of PR is-
A18 cmB19 cmC19.8 cmD21.86 cm
In a circle of radius 7 cm, tangent PT is drawn from a point P such tht PT= 24 cm. If O is the centre of circle, then find the length of OP.
View SolutionIn a circle of radius 7 cm, tangent PT is drawn from a point P such that PT=24 cm.If O is the center of circle then length OP=?
View SolutionIn the given figure , a smaller circle touches a larger circle at P and Passes through its centre O . PR is a chord of length 34 cm , what is the length (in cm ) of PS?

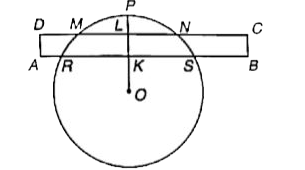
View SolutionIn the adjoining figure O is the centre of the circle. The radius OP bisects a rectangle ABCD, at right angle. DM=NC=2cm and AR=SB=1cmandKS=4cmandOP=5cm. What is the of the rectangle?
View SolutionAB is a tangent to a circle with centre O. If the radius at the circle is 7 cm and the length of AB is 24 cm, then what is the length (in cm) of OA?
View Solution