PQRST is a regular pentagon. If PR and QT intersects each other at X, then what is the value (in degrees) of ∠TXR?
98
90
72
108
The correct Answer is:D
To find the value of angle ∠TXR in the regular pentagon PQRST where lines PR and QT intersect at point X, we can follow these steps:
Step 1: Understand the properties of a regular pentagon
A regular pentagon has equal sides and equal angles. The measure of each internal angle in a regular pentagon is given by the formula:
Internal Angle=(n−2)×180n
where n is the number of sides. For a pentagon (n=5):
Internal Angle=(5−2)×1805=3×1805=108∘
Step 2: Identify the relevant triangles
In the pentagon PQRST, we can identify two triangles formed by the intersecting lines PR and QT:
- Triangle PQT
- Triangle PQR
Step 3: Analyze triangle PQT
Since PQ=PT (as sides of the regular pentagon), triangle PQT is isosceles. Let ∠PQT=∠PTQ=x. The sum of angles in triangle PQT gives:
∠TQP+∠PQT+∠PTQ=180∘
Substituting the known values:
108∘+x+x=180∘
108∘+2x=180∘
2x=72∘⟹x=36∘
Step 4: Analyze triangle PQR
Similarly, in triangle PQR, since PQ=QR, it is also isosceles. Let ∠QPR=∠QRP=y. The sum of angles in triangle PQR gives:
∠PQR+∠QPR+∠QRP=180∘
Substituting the known values:
108∘+y+y=180∘
108∘+2y=180∘
2y=72∘⟹y=36∘
Step 5: Find angle ∠TXR
Now, we can find ∠TXR which is equal to ∠PXQ because of the properties of intersecting lines. We can use the angles found in triangles PQT and PQR:
∠TXR=∠PQT+∠QPR=36∘+36∘=72∘
Conclusion
Thus, the value of ∠TXR is:
∠TXR=72∘
A regular pentagon has equal sides and equal angles. The measure of each internal angle in a regular pentagon is given by the formula:
Internal Angle=(n−2)×180n
where n is the number of sides. For a pentagon (n=5):
Internal Angle=(5−2)×1805=3×1805=108∘
In the pentagon PQRST, we can identify two triangles formed by the intersecting lines PR and QT:
- Triangle PQT
- Triangle PQR
Since PQ=PT (as sides of the regular pentagon), triangle PQT is isosceles. Let ∠PQT=∠PTQ=x. The sum of angles in triangle PQT gives:
∠TQP+∠PQT+∠PTQ=180∘
Substituting the known values:
108∘+x+x=180∘
108∘+2x=180∘
2x=72∘⟹x=36∘
Similarly, in triangle PQR, since PQ=QR, it is also isosceles. Let ∠QPR=∠QRP=y. The sum of angles in triangle PQR gives:
∠PQR+∠QPR+∠QRP=180∘
Substituting the known values:
108∘+y+y=180∘
108∘+2y=180∘
2y=72∘⟹y=36∘
Now, we can find ∠TXR which is equal to ∠PXQ because of the properties of intersecting lines. We can use the angles found in triangles PQT and PQR:
∠TXR=∠PQT+∠QPR=36∘+36∘=72∘
Thus, the value of ∠TXR is:
∠TXR=72∘
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IX)
Explore 5 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- X)
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VII)
Explore 6 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
If ABCDEF is a regular hexagon, then what is the value (in degrees) of ∠ADB?
A15B30C45D60PQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
A60B40C80D100In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQRand ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A50B60C80D100
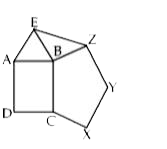
In the given figure, ABCD is a square, BCXYZ is a regular pentagon and ABE is an equilateral triangle. What is the value (in degrees) of ∠EBZ?
View SolutionMagnetic lines of force intersect each other .
View SolutionPQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
View SolutionCan two isothermal curves intersect each other?
View SolutionA circle passing through points Q and R of triangle PQR, cut the sides PQ and PR at point X and Y respectively. If PQ = PR, then what is the value (in degrees) of ∠PRQ+∠QXY ?
View Solution