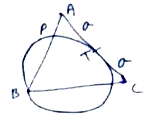
ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point Intersects AB at P. Then AP: AB is :
4:1
2:3
3:5
1:4
The correct Answer is:D
To solve the problem, we need to find the ratio AP:AB in the isosceles triangle ABC where AB=AC and a circle through point B touches line AC at its midpoint.
1. Identify the Triangle and Points:
- Let A be the vertex of the triangle, and B and C be the other two vertices such that AB=AC.
- Let M be the midpoint of AC.
2. Circle Touching AC:
- A circle passes through point B and touches line AC at point M.
3. Intersecting AB:
- The circle intersects line AB at point P.
4. Using the Power of a Point Theorem:
- According to the Power of a Point theorem, we have:
AP⋅AB=AM2
- Since M is the midpoint of AC, we can express AM in terms of AB:
AM=AC2=AB2
5. Substituting into the Equation:
- Substitute AM into the equation:
AP⋅AB=(AB2)2
- Simplifying this gives:
AP⋅AB=AB24
6. Solving for AP:
- Now, divide both sides by AB (assuming AB≠0):
AP=AB24⋅AB=AB4
7. Finding the Ratio:
- Now we can find the ratio AP:AB:
AP:AB=AB4:AB=1:4
Thus, the final answer is:
AP:AB=1:4
- Let A be the vertex of the triangle, and B and C be the other two vertices such that AB=AC.
- Let M be the midpoint of AC.
- A circle passes through point B and touches line AC at point M.
- The circle intersects line AB at point P.
- According to the Power of a Point theorem, we have:
AP⋅AB=AM2
- Since M is the midpoint of AC, we can express AM in terms of AB:
AM=AC2=AB2
- Substitute AM into the equation:
AP⋅AB=(AB2)2
- Simplifying this gives:
AP⋅AB=AB24
- Now, divide both sides by AB (assuming AB≠0):
AP=AB24⋅AB=AB4
- Now we can find the ratio AP:AB:
AP:AB=AB4:AB=1:4
AP:AB=1:4
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)
109 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)
35 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
In the figure, ABC is a triangle in which AB=AC. A circle through B touches AC at D and intersects AB at P. If D is the mid - point of AC, Find the value of AB :
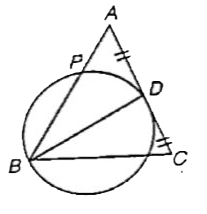 A2APB3APC4APD4√2cm
A2APB3APC4APD4√2cmIf ABC is an isosceles triangle with ∠C=90∘ and AC=5 cm, then AB is:
A5 cmB10 cmC5√2cmD2.5 cmΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
A60∘B90∘C120∘Dcan't be determined
ABC is an isosceles triangle with AB= AC. Draw AP⊥BC to show that ∠B=∠C.
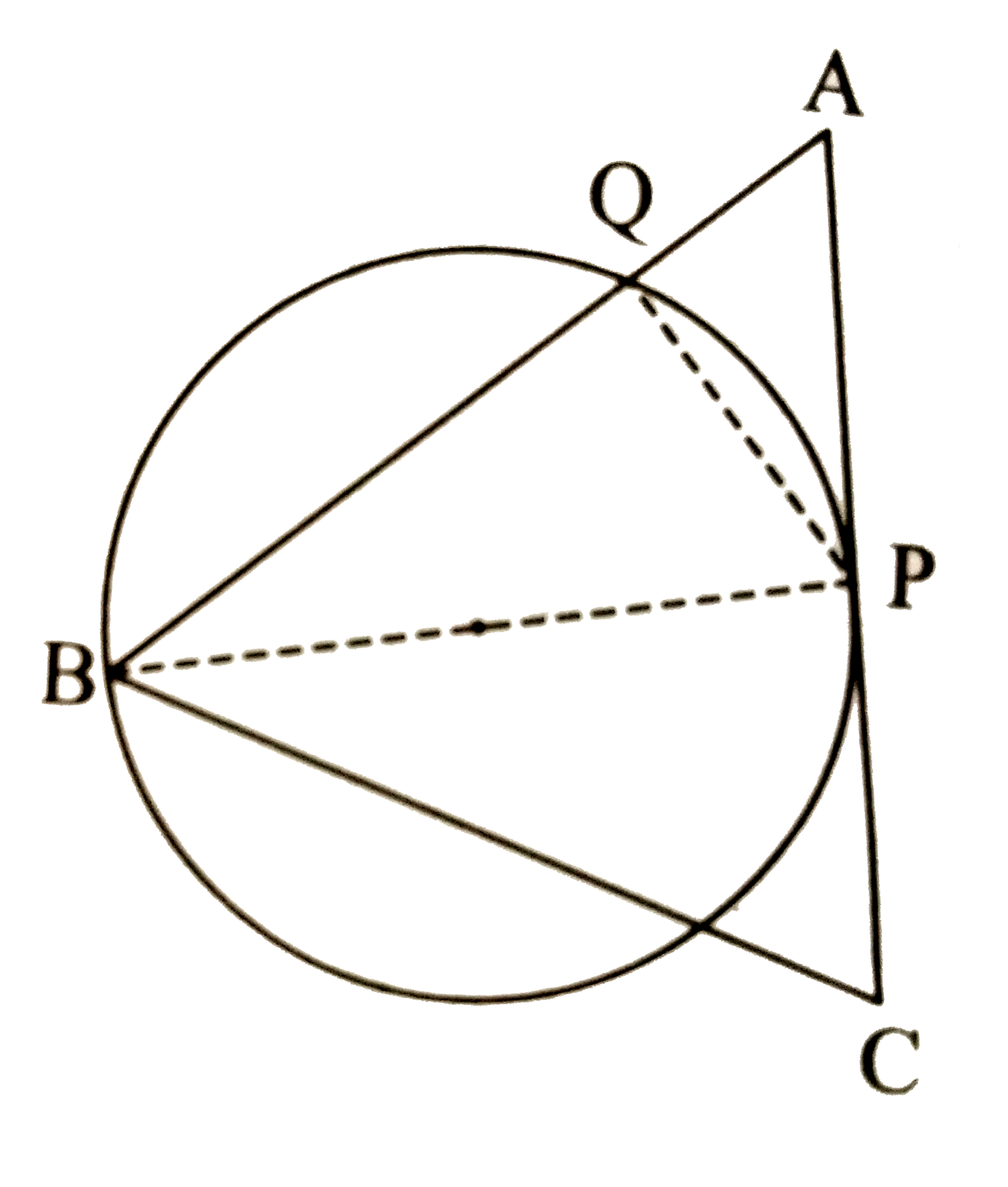
View SolutionIn ΔABC,AB=AC. A circle passing through B touches side AC at its midpoint P and intersects side AB at Q then prove BQ = 3AQ
Construction : Draw seg BP and seg PQ
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View Solution
ABC is an isosceles triangle with AB = AC. If AD = AE then choose the correct alternatives.
View Solution△ABC is an isosceles triangle with ∠C=90∘ and AC = 5 cm. Then, AB = ?
View Solution